

Investigation of Quadratics in the xb plane
by
Molade Osibodu
Objective: To show how to determine the roots of a quadrtric function by varying b.
Recall that the standard quadratic equation is wriiten in the form . Now consider the equation ax²+ bx + c where a = 1 and c = 1.
To determine the roots of the equation, it has to equal 0. Therefore, the equation we are concerned with is x²+ bx + 1 = 0. An animation of this equation by varying b is shown below.
Figure 1: Varying b in the equation y = x² + bx + 1
From figure 1 above, it shows that varying b shifts the graph along the x-axis. More detailed observations shown here.
We can also view a graph of this equation along the xb plane by solving for b. Solving for b gives the equation
b =( -x² -1)/x
A graph showing this equation is shown below
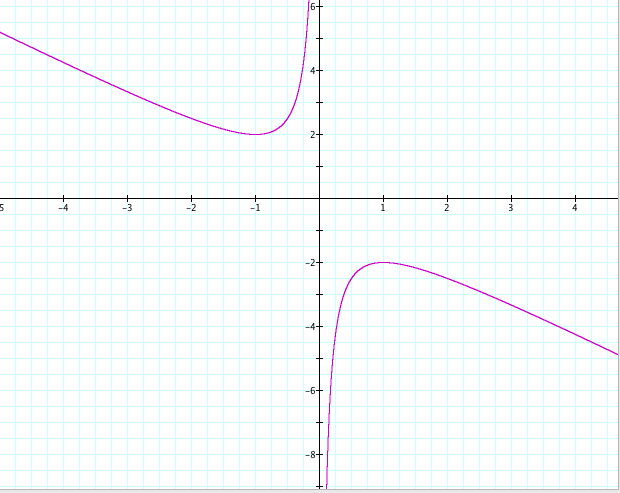
Figure 2: b = ( -x² -1)/x
Now lets investigate the graph when b is any number. Let b = 4
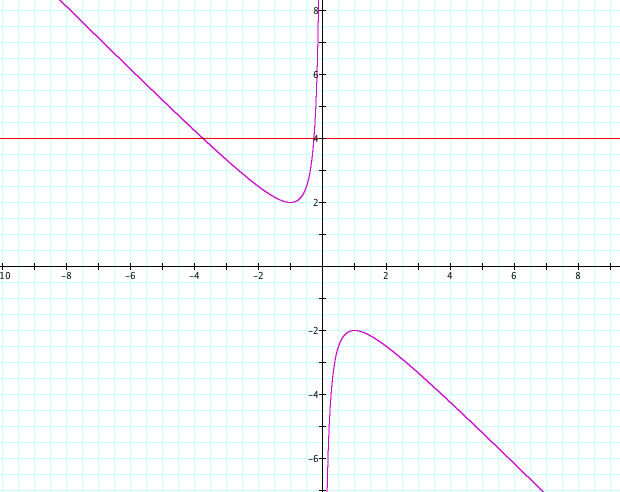
Now we see that we have two real roots at b = 4.
What happens if we change the sign of our equation from c = -1 to +1

Click here
We see that the y-axis still serves as a vertical assymptote to the graph. Now lets change the value of c and b also and investigate any differences
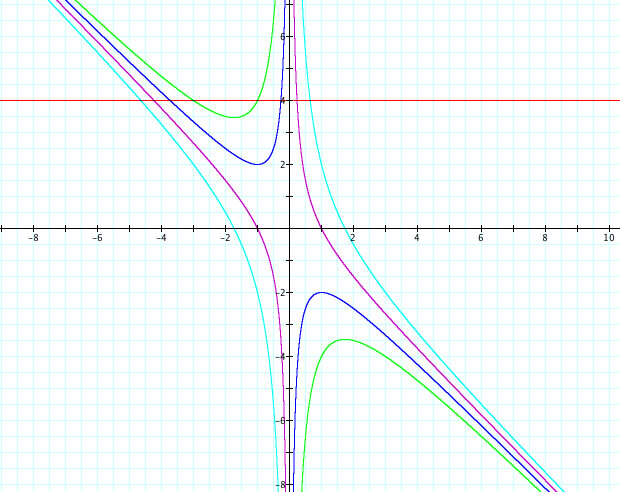
Click here
We see that the graph shifts but still uses the y-axis as the vertical assymptote. Furthermore, the zero's of the graph change.