

Exploring Triangle Medians
by
Molade Osibodu
Objective: To investigate properties of the medians of triangles
Let's start by constructing a triangle with it's median.
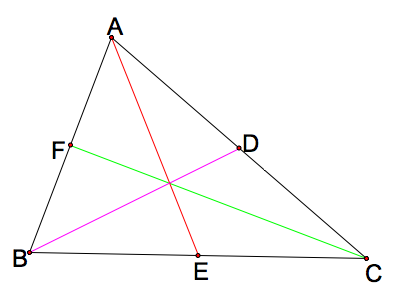
Triangle ABC has medians AE, BD and FC. Next, let's construct a triangle with the lengths of the median
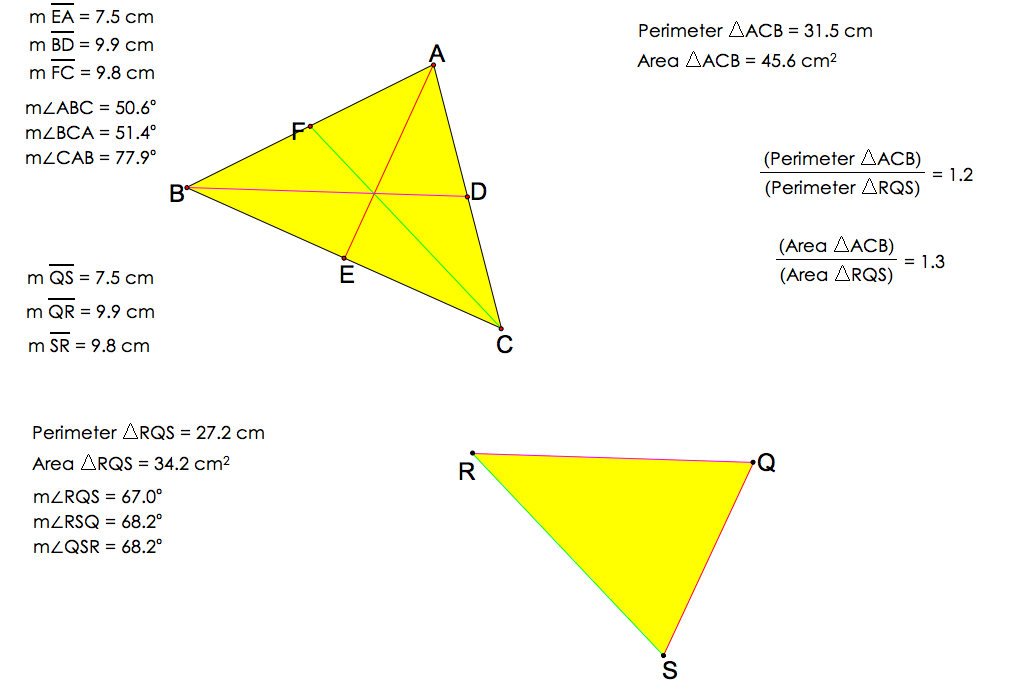
Next, let's investigate the relationship between the two triangles. Are they congruent? Similar? Do they have the same area? Do they have the same perimeter? WHat is the ratio of the areas and perimeters?
To see an animation, click here
From the above illustration, we can see that both triangles are neither similar, nor congruent. We also note that the ration of the perimeter is always between 1.0 and 1.2 while the ratio of the area remains constant at 1.3.
Let us further our observation by investigating what happens if the original triangle is an equilateral.
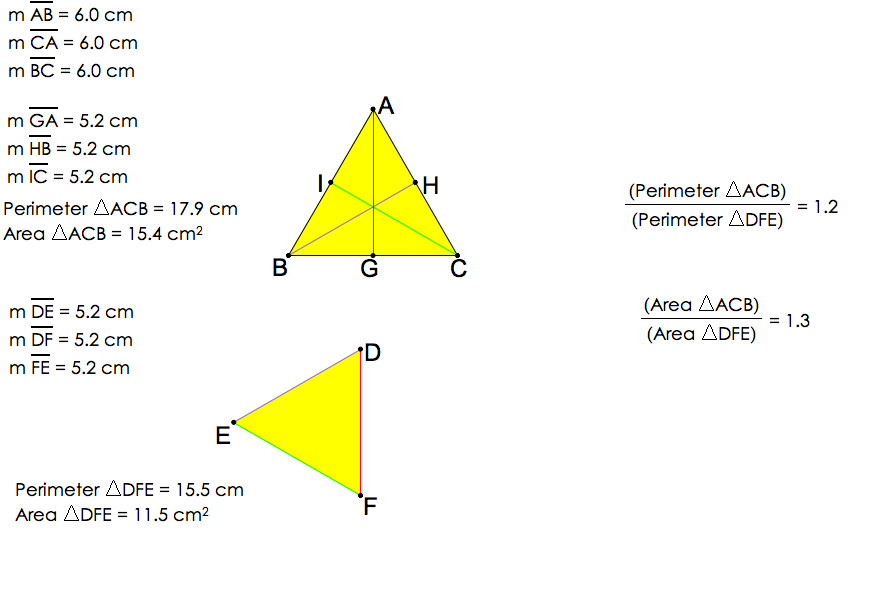
It is interesting to note that the median triangle is also an equilateral triangle. The previous properties are also evident in the equilateral triangle.
Now let's explore an isosceles triangle.
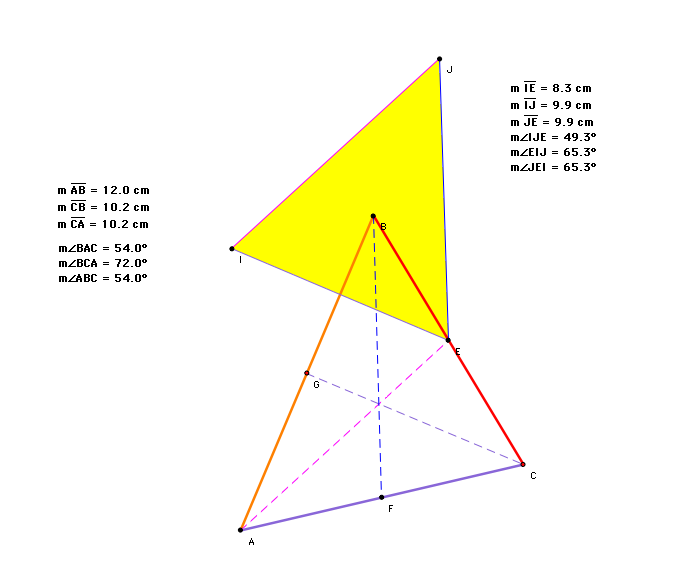
From the dimensions, we see that the median triangle(shaded), is also an isosceles triangle
To see an animation, click here
Let's find out if the same is true for a right triangle
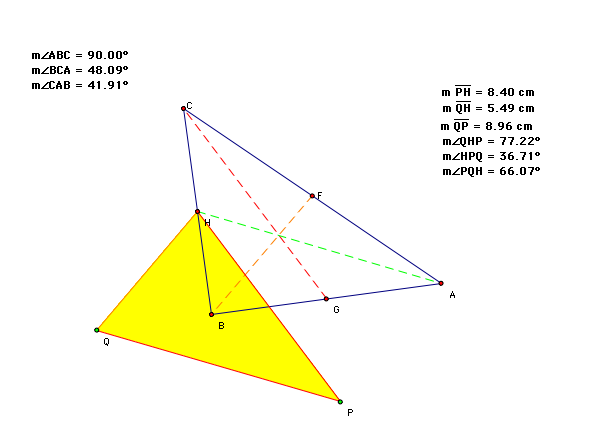
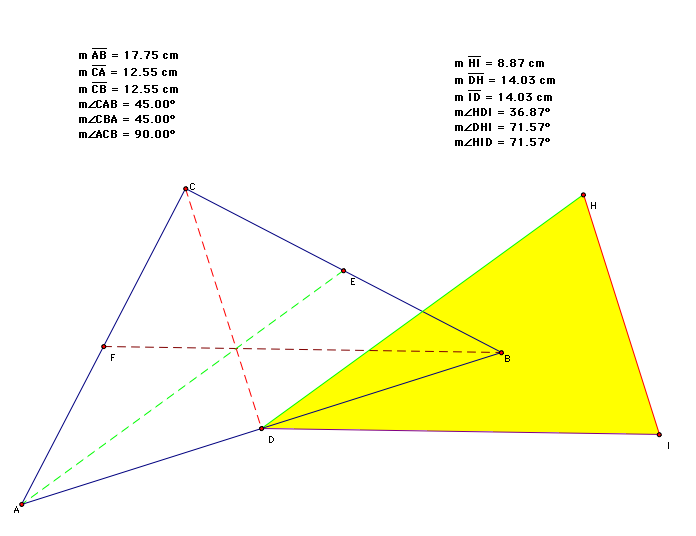
From the dimensions, we see that the median traingle (shaded), is not a right angle triangle. Even a right angled isosceles does not produce a right angle median as shown below
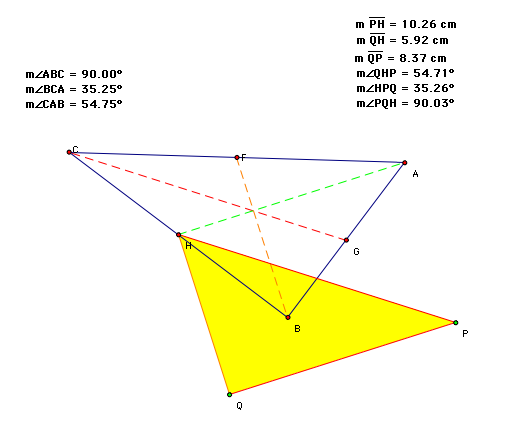
The only in which the original triangle and the median triangle are both right angled is the case when the first angle approaches 90 degrees, the second approaches 35.3 degrees and the third approaches 54.7 degrees for both triangles.
To see an animation, click here