

Altitudes and Orthocenters
by
Molade Osibodu
Objective: To show the relationship between altitudes of a triangle and circumcenters of a circle.
To begin, create the orthocenter H of triangle ABC. Recall that the orthocenter is the intersecting point created by constructing the perpendicular line from the three vertices to the opposite sides as shown below:
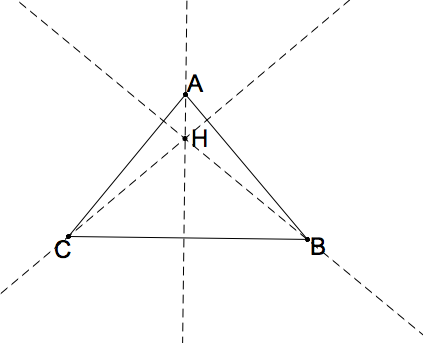
Figure 1: A triangle showing orthocenter H
Then, create triangle HAB, HBC and HCA.
Next, create the orthocenter for the new triangles.
Then draw the circumcenter for our original triangle and the three new triangles. Recall that the circumcenter is the intersecting point created by constructing the perpendicular line from the midpoint of each side with the corresponding side of the triangle as shown below:
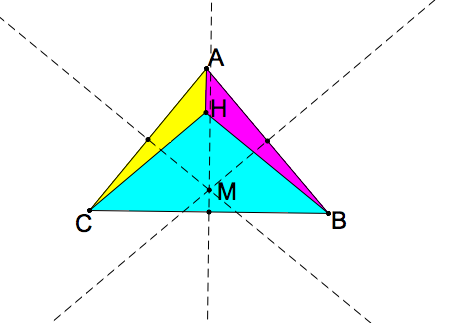
Figure 2: A triangle showing orthocenter H and circumcenter M
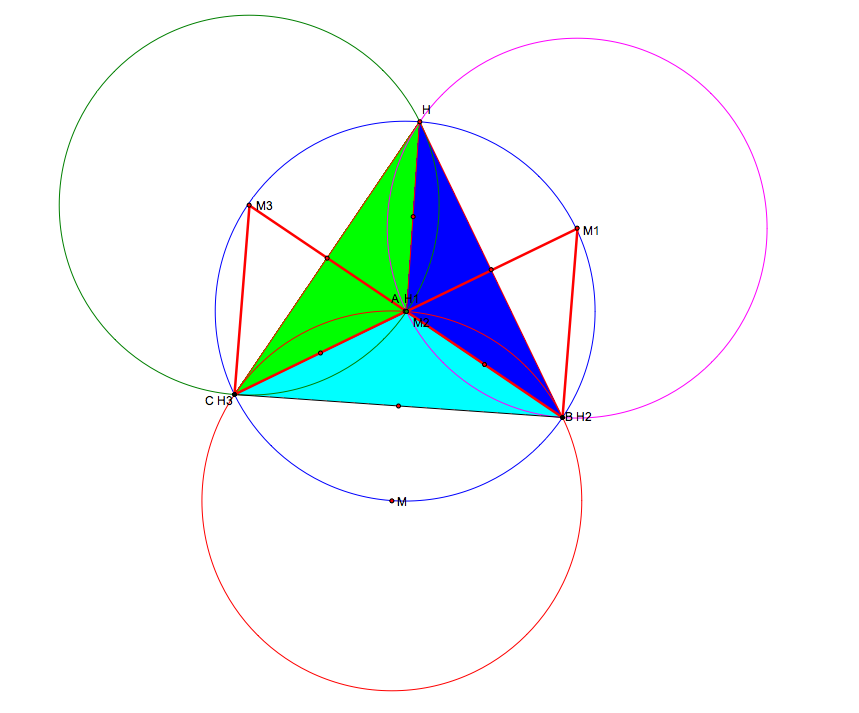
Finally, create the circumcircle from each of the four circumcenters. The final product is shown in the figure below
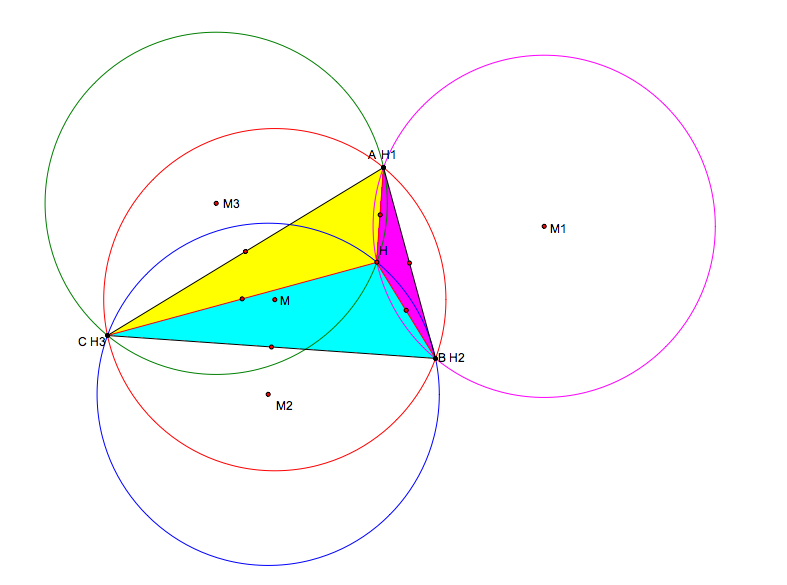
Figure 3: Circcumcircles with circumcenter M, M1, M2 and M3
Creating a line joining the vertices of the original triangle to the circumcenters creates a hexagon.
Observations
In creating the final figure, several conjectures was formulated. They are listed below:
(i) The orthocenter of triangles HAC, HAB and HBC are located on the vertices of the original triangle (see figure 3)
(ii) The line formed formed from the vertices of the original triangle to the circumcenters form the radii of each circle
(iii) The radii of the circle are all equal, hence the area of all the circles are equal
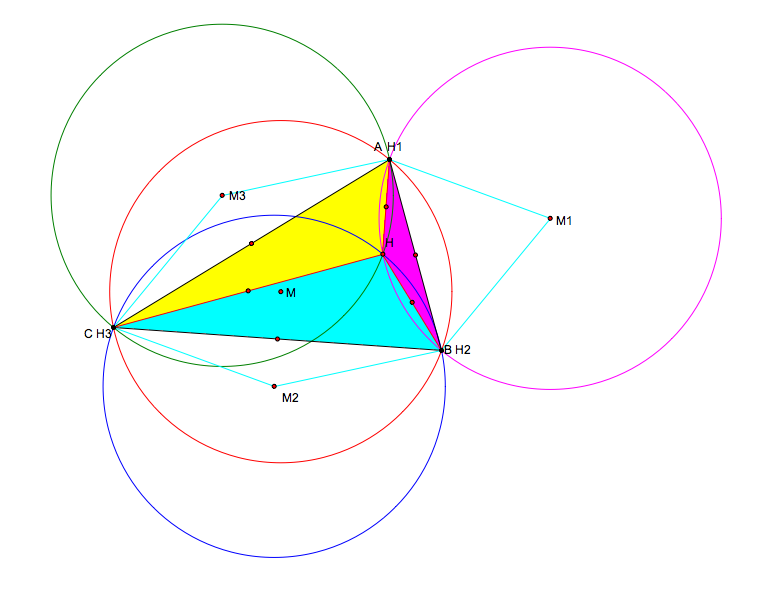
(iv) Moving any of the vertices of the original triangle to H, forms a rectangle as shown below
(v) The area of the formed rectangle or the hexagon is twice the area of the original triangle
(vi) The area of triangle AH1BH2CH3 is half the area of the rectangle
(vii) Moving any of the vertices of the original triangle to the circumcenter on the opposite side forms two congruent triangles as shown below
In conclusion, we have shown various conjectures that could be made from the altitude or vertex and the circumcenter of a triangle. Click here to see the gsp sketch and to prove conjectures are true