

Exploring Pedal Triangles
by
Molade Osibodu
Objective: To show the relationship between pedal triangles and centers of triangles.
Let's begin by showing how to create a pedal triangle.
Step 1. Create a triangle on GSP using lines as shown below:
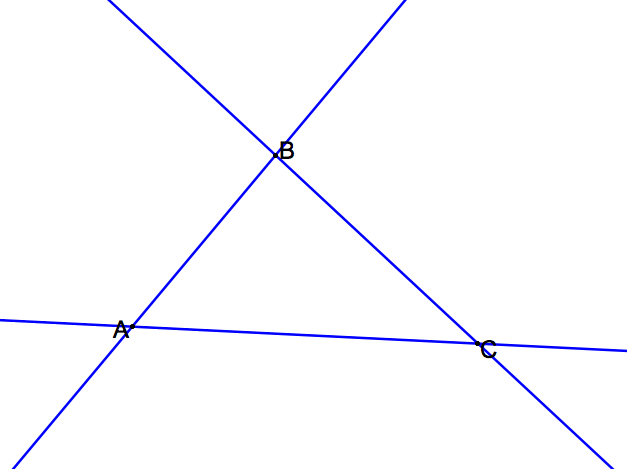
Step 2: Create an arbitrary point P and draw a line perpendicular from the 3 sides of the triangle to the point as shown below:
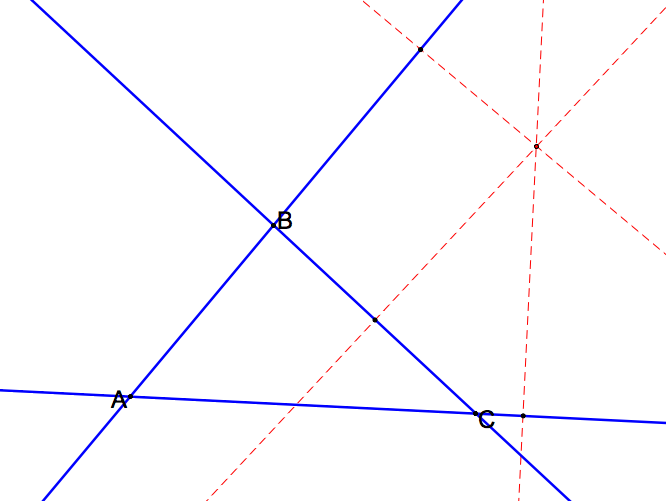 '
'
Step 3: Connect the intersection point to show the triangle as shown below:
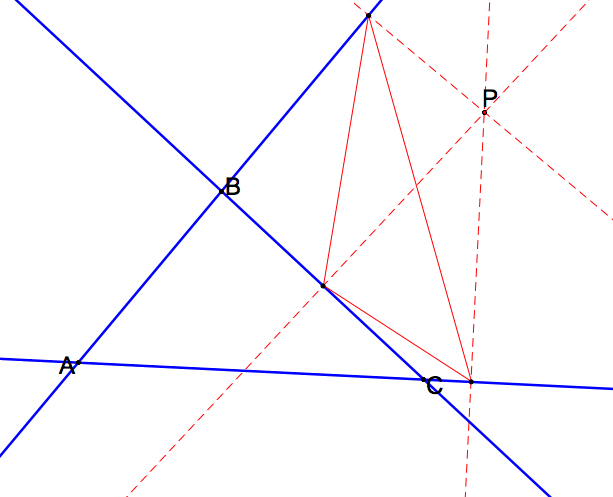
This triangle is known as the Pedal Triangle. The figure below shows the triangle, the pedal triangle and the point P.
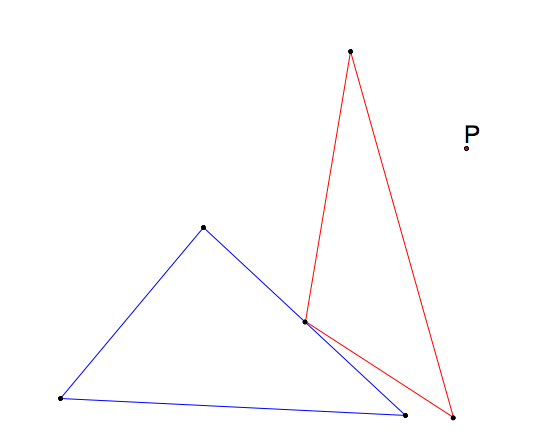
Next, we will examine what happens when the pedal point touches centers of triangles.
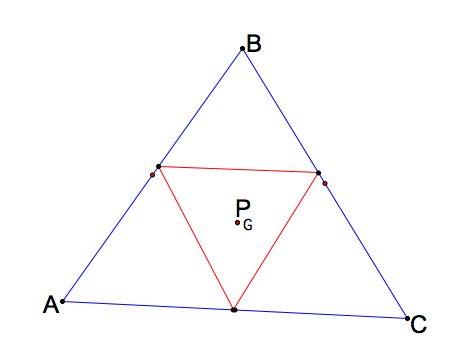
What happens when the pedal point P is the centroid (RECALL) of triangle ABC?
 |
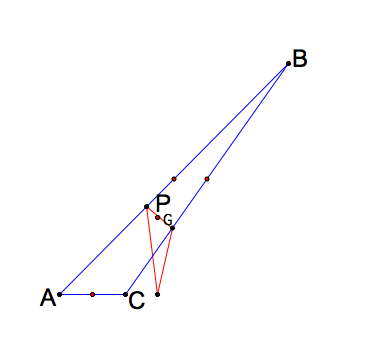 |
In some cases, the pedal triangle stays inside triangle ABC and in others, one vertex remains outside. Click here for GSP
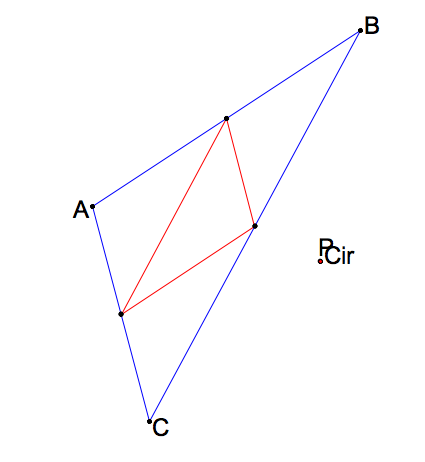
What happens when the pedal point P is the circumcenter (RECALL) of triangle ABC?
 |
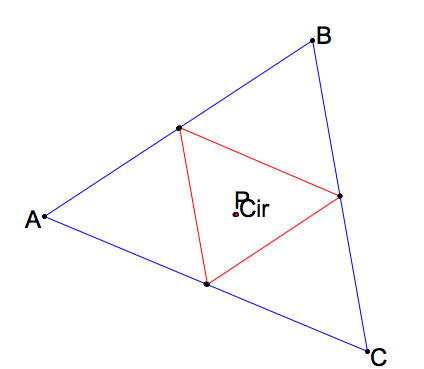 |
We see that whether the circumcenter is inside or outside of the triangle, the pedal triangle still stays within traingle ABC.When the Pedal point is at the circumcenter, the feet of the perpendiculars to the sides by definition of the Pedal point and the construction of a circumcenter must be at the midpoints of the sides of the triangle. Therefore the pedal triangle is the MEDIAL triangle of the original
Click here for GSP
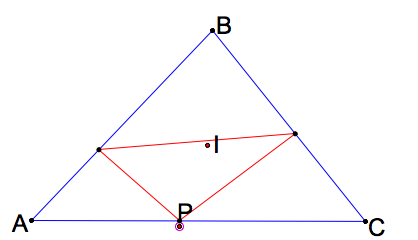
What happens when the pedal point P is the incenter (RECALL) of triangle ABC?
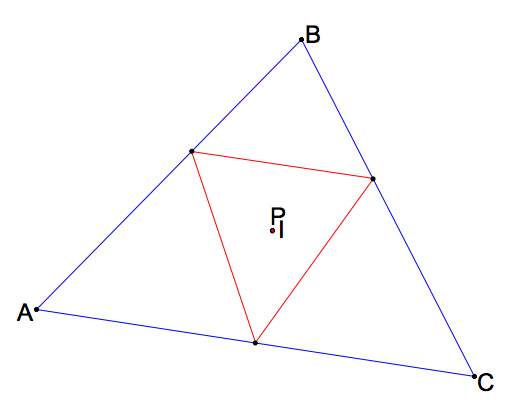
The pedal triangle would always stay within triangle ABC. The geometric relations there let you
prove that it is the ORTHIC triangle. Click here for GSP
What happens when the pedal point P is the orthocenter (RECALL) of triangle ABC?
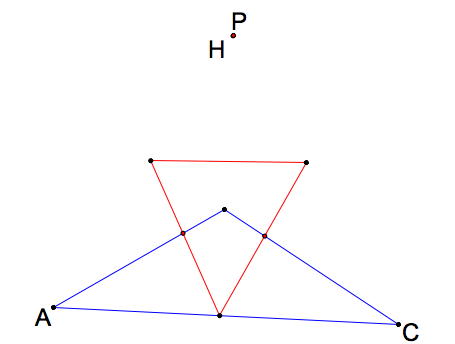 |
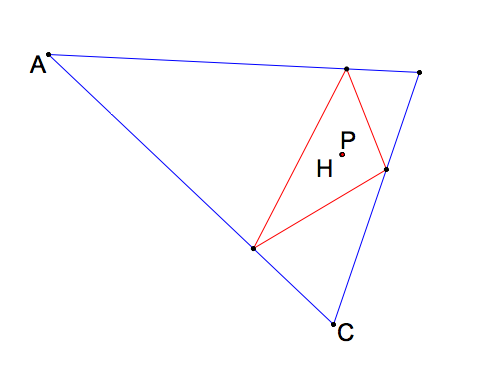 |
The pedal triangle would always stay within triangle ABC when the orthocenter in inside. However, when the orthocenter is outside, only one vertex of the pedal triangle stays inside the triangle. Click here for GSP
What happens when the pedal point P is the nine point circle (RECALL) of triangle ABC?
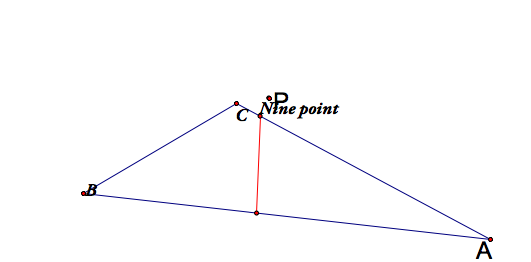 |
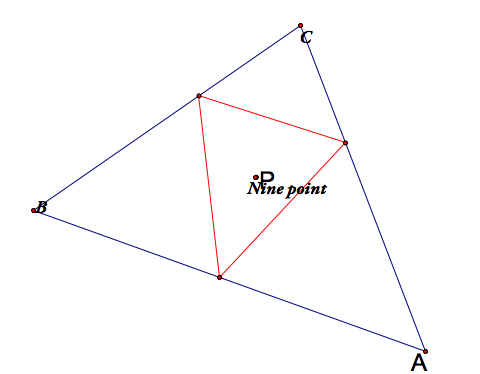 |
When the nune point circle in outside, the pedal triangle becomes degenerate and when it is inside, the pedal triangle is also inside triangle ABC. Click here for GSP
What happens when the pedal point P is one of the vertices of triangle ABC?
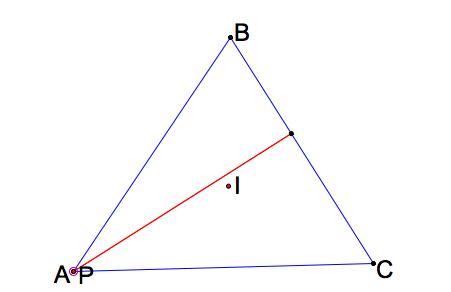 |
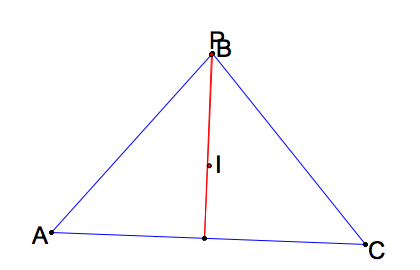 |
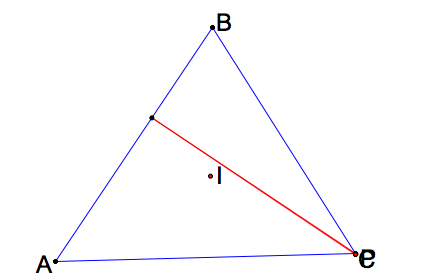 |
In all three cases, the pedal triangle become degenerate. Click here for GSP
What happens when the pedal point is on any side of triangle ABC
The pedal triangle stays withing triangle ABC. Click here for GSP
In conclusion, the pedal triangle has many different characteristics when placed on the different centers of a triangle