Assignment 10: Problem 9
Jason P. Pickhardt
Problem:
Investigate the
following for 
Describe when a = b, a < b, and a > b.
Exploration:
The first part of the exploration asks for the graph of the parametric
function, from. At first glance this may not look familiar at all however
the function given is the staple of trigonometry learned in high school
mathematics. When a=b=1 on the given
interval we have what is known as the unit circle. Also, due to the interval we
know that there is one and only one complete circle generated by the parametric
equation.
a=b
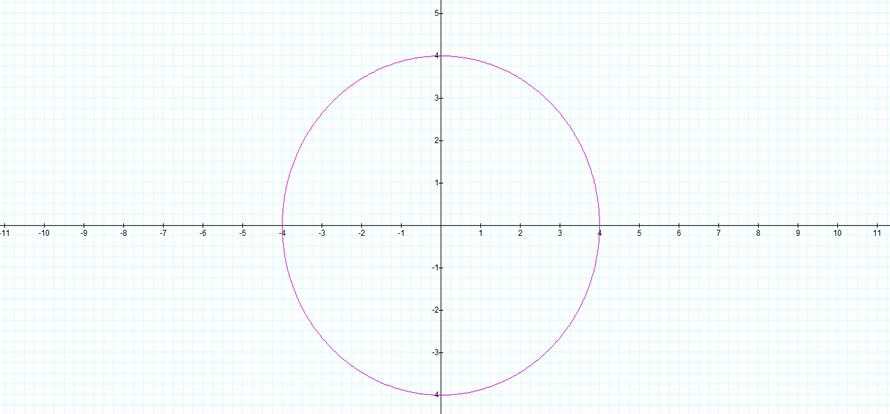
We can analyze why this is true further using the figure below and see how trigonometry can be used to define our circle with radius, r. If we take the cosine and sine of the angle formed by leg x and hypotenuse r we will wind up with:
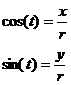
Written another way we get:
We can see how our parametric equation was originally developed and that when a=b=r we have a circle with radius r defined by our parametric equation. Therefore we can say that when r is something different than 1, we will have a circle of radius r centered about the origin.
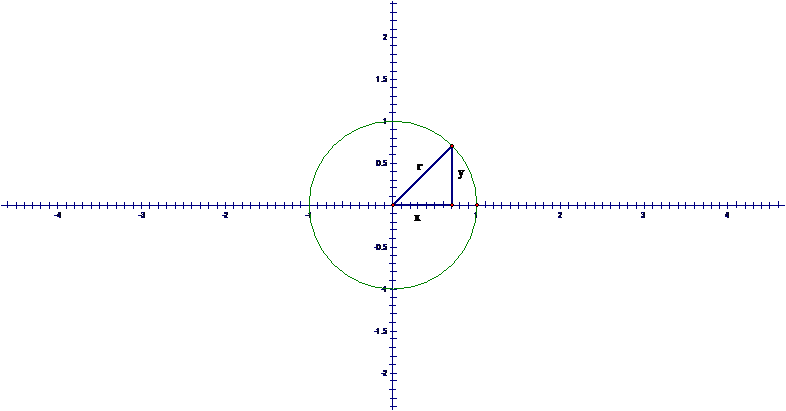
When we have the case where a<b there is a different result from when both are equal. Instead of getting a circle we produce an ellipse centered at the origin as shown below with its major axis in the y direction and minor axis in the x direction. The parameter a defines the semi-minor axis while b defines the semi-major axis. That is to say that the distance from the origin to the ellipse in the x direction is a and the distance in the y direction is b.
a<b
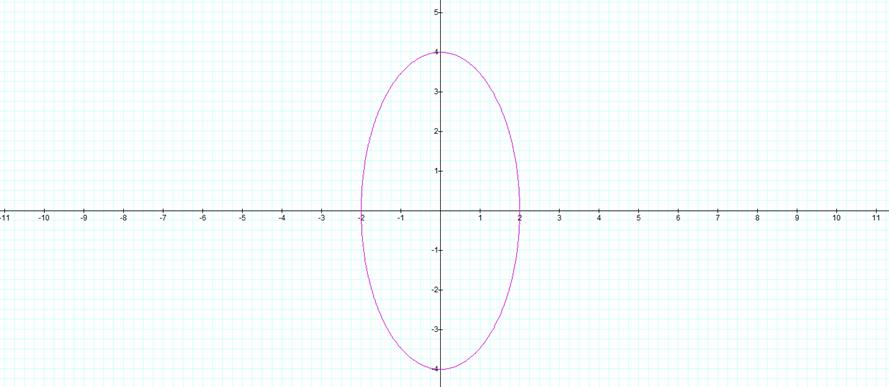
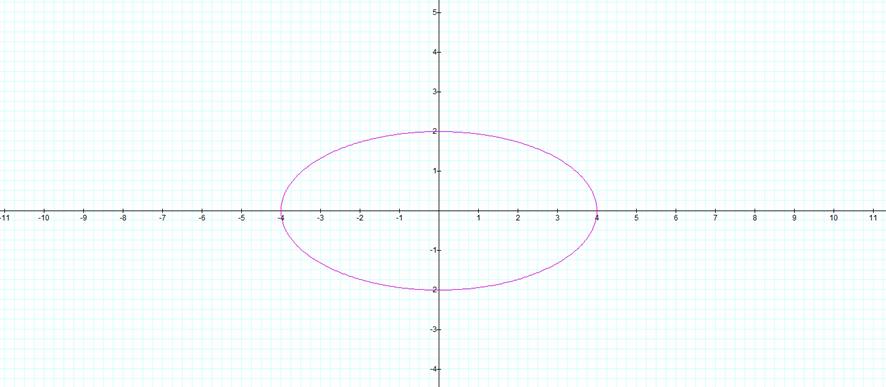
Similarly, when we have the case where a>b we get an ellipse with the conditions opposite to the previous case. So we can say that the length of the semi-major axis is a and in the x direction. Also, the length of the semi-minor axis is b and in the y direction.
a>b
Conclusion:
Using right triangles and trigonometry we were able to discover why the parametric function described is a circle when the parameters a=b. Also, we discovered that when these parameters were not equal we have an ellipse whose major and minor axes are dependent on the parameters a and b.