
Assignment 6: Problem 5
Jason P. Pickhardt
Problem:
The football rules in college football were changed a few years ago have made the uprights 5 feet narrower than previously. Many game commentators have harped about how much harder it is to kick field goals from the hash marks. Assume the field goal is attempted from the hash marks. At what yard marker does the kicker have maximum angle to the two uprights. Note: You will need to find out the width of the uprights and the width of the hash marks . . . make a sketchpad model. Is there any merit to some commentator’s argument to take a penalty in order to have a "better angle" on the field goal kick?
Exploration:
While investigating this problem I used a web search for football field dimensions and found the following website to be very useful: http://www.sportsknowhow.com/football/field-dimensions/ncaa-football-field-dimensions.html. The most important dimensions I was able to find from this site are:
Width of field: 160’
Width of hash marks: 40’
Width of uprights: 18.5’
Using these dimensions and some prior knowledge of a football field I was able to construct a GSP sketch (shown below) of a field in order to model the given situation.
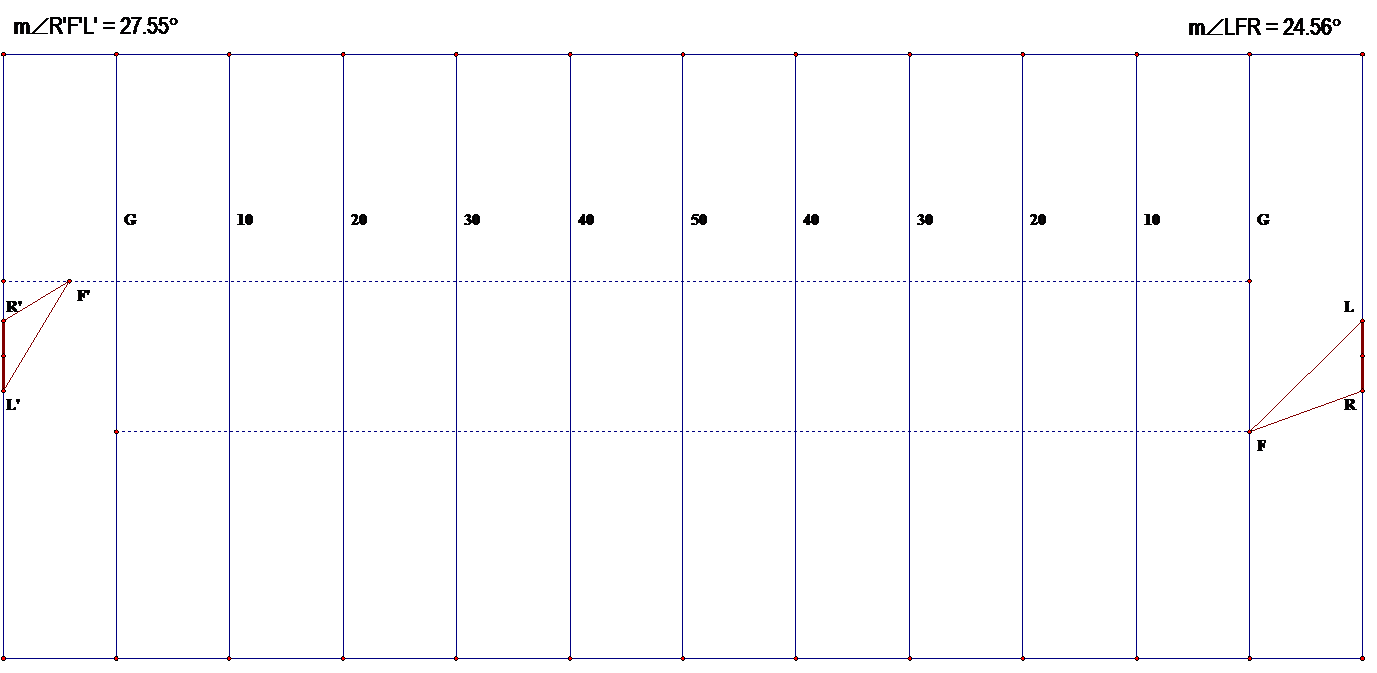
The first step I took in analyzing this problem was to construct a dynamic point F to represent the placement of the football on one of the hash marks. From here I was able to create segment between point F and the right (R) and left (L) uprights. The angle that we are talking about in this problem is the angle at vertex F of the triangle formed with the uprights when drawing these segments. By simply moving F along the hash mark line we can see that the greatest angle to the uprights is when the ball is placed at the goal line. Realistically speaking this can never happen. Even if a team had the ball at the one inch line on fourth down they would still have to kick the ball from the seven yard line based on NCAA Football rules which places the holder seven yards from the line of scrimmage.
Though the hash marks do not extend to the back of the end zone for explorations sake I took the liberty of studying what would happen if I did so. Point F’ will be our new football location if the hash marks went through the end zone. When moving this point along the hash we find a maximum angle of 27.55 somewhere inside of the end zone. This information combined with the first exploration would tell us that the closer to the uprights the ball is placed, the larger the angle. Thus, it is mathematically incorrect to take a penalty for delay of game to back the kick up 5 yards. However, there is validity to the idea of running a play in order to kick the ball from the center of the field as long as said kicker can kick straight. A copy of the GSP document can be found here in order to see the dynamic points F and F’ and their respective angle measurements.
Conclusion:
It seems in this problem that announcers are confusing the idea of backing up a field goal with the concept of backing up a punt. Many times a team will take a delay of game penalty to back a punt up 5 yards so that the punter will not kick the ball into the end zone but within the 5 yard line. This indeed brings up an extension of this problem and whether or not a team should take a penalty on a punt and at what yard marker it makes sense to do so. With all this said it is never a good idea to back up a field goal. There is a reason why extra points are rarely missed and that is because they are closer to the uprights.