
Final Assignment
Jason P. Pickhardt
Problem:
Grazing area
Farmer Jones had a goat on a tether. He tied the end of the tether not attached to the goat to a stake in a field. Over what area could the goat graze? Of course you need to know something about the length of the tether and about the field.
There are two structures in the field:
-- a shed that is 20 ft long and 20 feet wide (square)
-- a silo that is 20 ft in diameter
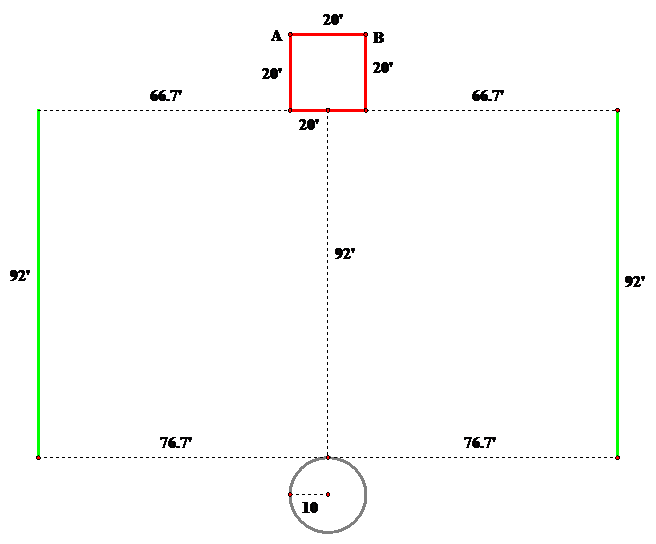
The center of the shed and the center of the silo are on a line and the distance apart is 92 feet. The distance from center to center, if you wanted to use this data, is 112 feet. The tether for the goat is 76.7 feet long. The stake to which the tether is tied is somewhere along the line of centers between the shed and the silo. Explore the area over which the goat can graze as the stake is moved along this line segment from the midpoint of the side of the shed to the edge of the silo.
Exploration:
There are many ways that one might choose to explore this problem. One interesting thing to explore here would be finding where to place the stake along the given line that would maximize the amount of grass that the goat could graze. Also, it would be possible to analyze case by case what area of grass would be able to be grazed at locations such as directly at the barn or the shed, or at the midpoint of the line between them and so on. However, the way I attacked this problem was to think that maybe the goat is connected to a clothes line where he could walk from barn to silo and graze all of that possible area. Thus we have three cases to analyze in order to find the over all area the goat can graze. First letís look at the possibility of the goat being staked at the midpoint of the barn and how much area he can reach around all other sides of the barn. The following is a GSP sketch made in order to model and calculate the areas.
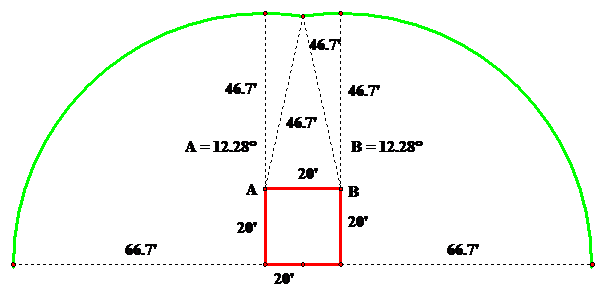
As can be seen in the sketch, we need to quantify the area of two quarter circles, a isosceles triangle and two sectors of a circle. The calculations are as follows:
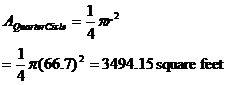
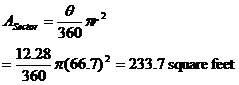
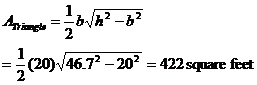
Of course we need to take both the sector and quarter circle into account twice as. Thus the overall grazing area becomes:
![]()
Another portion to calculate is the area of grass between the barn and the silo that the goat can graze. The goat can go straight out in both directions the entire length of the tether (76.7í) an will cover a rectangular area as shown below. The calculation is very simple and follows the illustration.
![]()
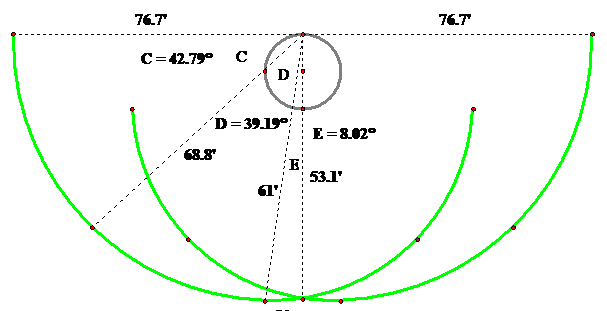
As shown above there is one area left to be calculated that the goat can graze. This area is not so easy to calculate with the silo being round and thus there was some approximation done in order to make this calculation. We can estimate the radius of circular sectors at eighths of the circumference. This is done by subtracting an eighth of the circumference first from the original length of the tether. This is continued at each eighth of the circumference. The results are sectors defined by angles C, D and E and the accompanying radii shown. It is important to note that the following are approximations as the radius of each sector is not similar throughout as the radius will decrease slightly while the goat walks around the silo.
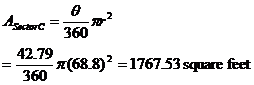
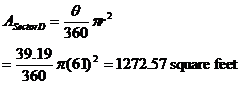

It remains to double the areas of the sectors for both sides of the silo as well as subtracting the area of grass that the silo actually sits on. The result is as follows:
![]()
Conclusion:
We have calculated the three different areas over which the goat can graze. Again, there are many ways to look at this exploration and this is simply one way. After all of these calculations we can combine the areas to find the total area over which the goat can graze.
![]()