
Triangle Centers
by
Cori Pringle
The medians of a triangle are concurrent at the centroid, which is at a point 2/3 of the distance of each median. See proof below:
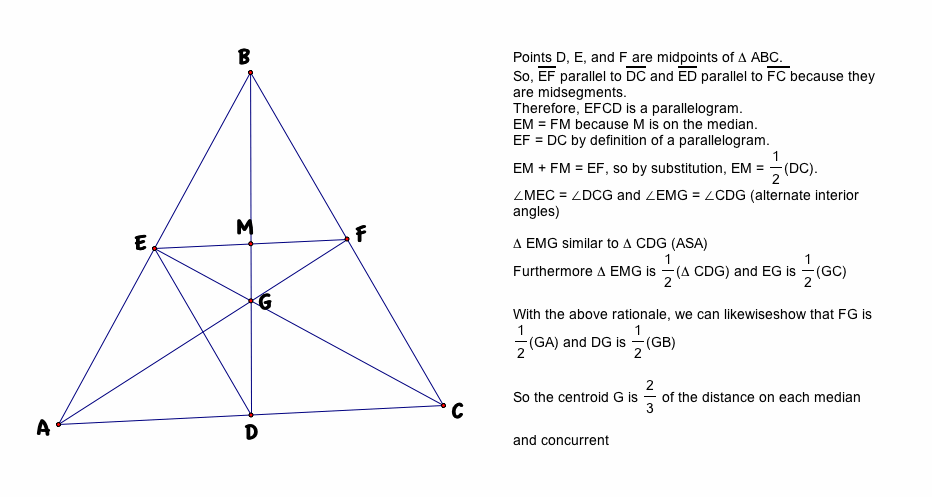

Triangle Centers
by
Cori Pringle
The medians of a triangle are concurrent at the centroid, which is at a point 2/3 of the distance of each median. See proof below:

In Math I, students are to learn about triangle centers:
MM1G3. Students will discover, prove, and apply properties of triangles, quadrilaterals, and other polygons.
c. Understand and use congruence postulates and theorems for triangles (SSS, SAS, ASA, AAS, HL).
d. Understand, use, and prove properties of and relationships among special quadrilaterals: parallelogram, rectangle, rhombus, square, trapezoid, and kite.
e. Find and use points of concurrency in triangles: incenter, orthocenter, circumcenter, and centroid.To introduce triangle centers to students, I would use GSP. For students to understand the relationship of the medians to the centroid, I would have students explore the properties using GSP. I would encourage them to make measurements of the lengths of the segments and notice any relationships between them. Students should then make conjectures of their findings and I would check to make sure they have found the 2/3 relationship in one way or another.
I recently read an article about students misconception of proof and would assume many of my students would find the above investigation a proof of my original statement:
The medians of a triangle are concurrent at the centroid, which is at a point 2/3 of the distance of each median.
It would be my goal to take this opportunity to show students how to "prove" their findings. The above proof is simple enough for high school freshmen to understand. The properties of parallelograms should have been covered in this course, as well as the triangle congruence theorems. Similarity is covered in middle school, so the jump from congruence to similarity should not be a big leap. I am not sure many students would be able to complete the entire proof on their own, but working in small groups, students should be able to provide a reasonable argument.
I also feel that students would benefit greatly from each group sharing their work with the class. Students could create posters of their proofs or we could use a document camera projected on the SMART board to provide a visual for the other students. This would allow the entire class the opportunity for a discussion of the thoroughness of each argument. Students could really learn a lot from each other.