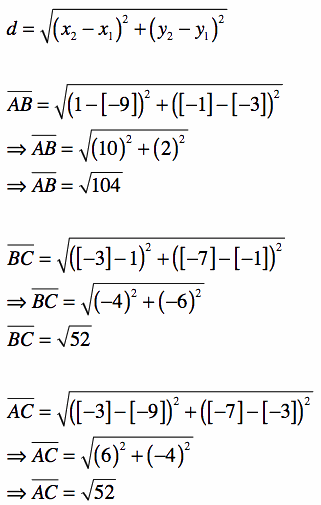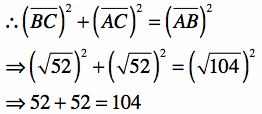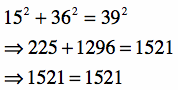Pythagorean Theorem & its Converse
by
Mike Rosonet
Goals: Students should know what the Pythagorean Theorem says and how to use it for solve for any missing side length of a given right triangle. Students show also have an understanding of what a Pythagorean Triple is and how to determine if a set of 3 numbers qualifies to be a Pythagorean Triple.
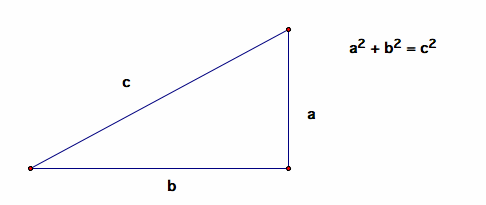
Lesson: The Pythagorean Theorem states that, if a triangle is a right triangle, then the sum of the squares of its legs equals the square of its hypotenuse. It oftentimes is stated like so:
Given the following triangle, the Pythagorean Theorem is
Example 1: Solve for x.
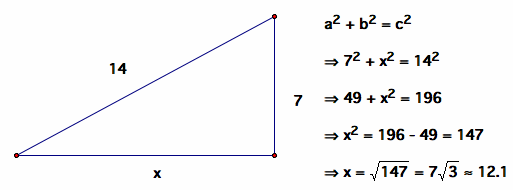
Therefore, the length of the base x of the triangle is approximately 12.1.
The Converse of the Pythagorean Theorem states that, if 
is true, then the given triangle is a right triangle.
Example 2: Verify that triangle ABC is a right triangle, given that the coordinates of its vertices are: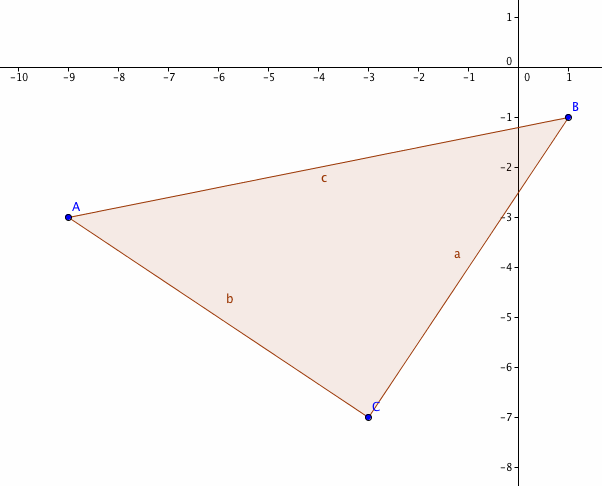
A(-9, -3), B(1, -1), C(-3, -7)
Triangle ABC will have sides AB, BC, and AC, as shown in the figure to the right. (This figure was made using the software program GeoGebra. For more information, click here.) Therefore, students will need to recognize that the only way to determine the lengths of these sides is to use the distance formula.
Thus, triangle ABC is indeed a right triangle.
Pythagorean Triple: 3 whole numbers that satisfy the Pythagorean Theorem, where the greatest number is the length of the hypotenuse.
A few common Pythagorean Triples:
3, 4, 5
5, 12, 13
7, 24, 25
8, 15, 17
Example 3: Determine if the following set is a Pythagorean Triple.
15, 36, 39
Hence, the set {15, 36, 39} is a Pythagorean Triple.
Homework: Determine if the following sets can be the lengths of the sides of right triangles using Pythagorean's Theorem. Then, determine if the set is a Pythagorean Triple.
Hint: recall the definition of a Pythagorean Triple...
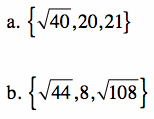
Solution:
a. the set 
does not contain numbers that can be the side lengths of a right triangle
Furthermore, because all 3 numbers are not whole numbers, the set is not a Pythagorean Triple.
b. the set 
does contain numbers that can be the side lengths of a right triangle.
However, because all 3 number are not whole numbers, this set, which does create a right triangle, is not a Pythagorean Triple.