Parametric Equations
by
Mike Rosonet
A parametric curve in the plane is a pair of functions
x = f(t)
y = g(t)
where the two continuous functions define ordered pairs (x, y). The two equations are called the parametric equations of a curve. The extent of the curve depends on the range of t. In many applications, x and y are thought to be "varying with time t" or the angle of rotation that some line makes from an initial location.
Various graphing technology, such as graphing calculators or graphing computer software, can be easily used with parametric equations. This investigation of parametric equations will use the program Graphing Calculator 3.5, which is considered to be one of the most friendly graphing software programs available.
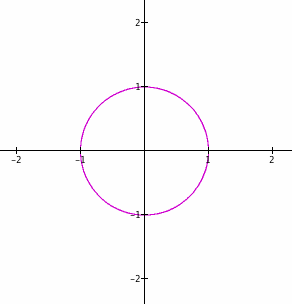
Consider the graph of the parametric equations:
x = cos (t)
y = sin (t)
![]()
As seen from the graph, these are the parametric equations of a circle. In order to investigate these equations deeper, it's necessary to apply constant values at different positions in the equations.
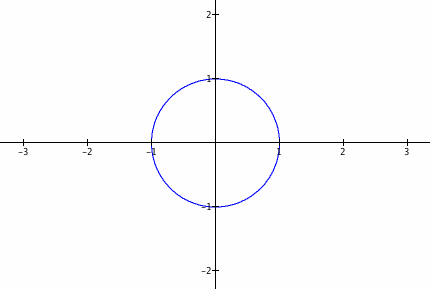
What if the constants a and b were placed as coefficients of t ?
x = cos (at)
y = sin (bt)
![]()
Let a = b = 2.
This graph is the same as the graph of the parametric equations without the constants a and b. Is this due to the fact that a = b?
To investigate, let the value of a vary from a = 0 to a = 6, and b = 1.
When a = 0, the graph is a line segment at x = 1from y = -1 to y = 1. Again, when a = 1, the graph is of a circle, as was initially investigated. As the value of a increases from a = 0 to a = 6, the graph reveals the graph of x = cos y from y = -1 to y = 1 with a decreasing period; this decreasing period causes the graph of cosine to occur multiple times within the parameters of y = -1 to y = 1.
Now, let a = 1 and the value of b vary from b = 0 to b = 6.
When b = 0, the graph is a line segment at y = 0 from x = -1 to x = 1. Again, when b = 1, the graph is of a circle, as was initially investigated. As the value of b increases from b = 0 to b = 6, the graph reveals the graph of , the graph reveals the graph of y = sin x from x = -1 to x = 1 with a decreasing period; this decreasing period causes the graph of sine to occur multiple times within the parameters of x = -1 to x = 1.
What if the constants a and b were placed as coefficients of the equations?
x = a cos (t)
y = b sin (t)
![]()
Let a = b = 2, just as the previous investigation.
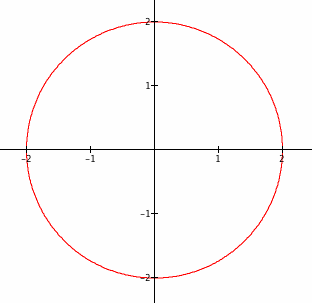
It appears that, by placing the constants a and b as coefficients of the equations, a and b expand the distance from the roots of the graph and the y-intercepts of the graph from its center at the origin. What happens when a and b vary?
To investigate, let the value of a vary from a = 0 to a = 4, and b = 1.
When a = 0, the value of the parametric equation for x equals 0 when t = 0, and the value of the parametric equation for y equals 0 when t = 0, regardless of the value of b because the sin (0) = 0. Hence, there is no graph when a = 0. Furthermore, as the value of a increases to a = 1, the graph approaches the initial graph of a circle. However, as the value of a increases beyond a = 1 to a = 4, the graph becomes an expanding ellipse with an expanding major axis along the x-axis and a constant minor axis along the y-axis from y = -1 to y = 1.
Now, let a = 1, and the value of b vary from b = 0 to b = 3.
When b = 0, the value of the parametric equation for x equals 1 when t = 0 because the cos (0) = 1, and the value of the parametric equation for y equals 0 because of the value of b. Hence, the graph is a line segment from x = -1 to x = 1 when b = 0. Furthermore, as the value of b increases to b = 1, the graph approaches the initial graph of a circle. However, as the value of b increases beyond b = 1 to b = 3, the graph becomes an expanding ellipse with an expanding major axis along the y-axis and a constant minor axis along the x-axis from x = -1 to x = 1.
Thus, the position of a and b determine the transformation of the initial graph of a circle. When a and b are coefficients of t, they affect the number of periods of the graphs of x = cos y and y = sin x within the parameters of the values of a and b. When a and b are coefficients of the equations, they affect the length of the major axes of the ellipses formed as the values of a and b increase and decrease.