Parabola Translations

by

Mike Rosonet

Parabolas can be translated, or moved, about the coordinate plane by manipulating different values of the vertex form its function. Consider the graph of the parabola

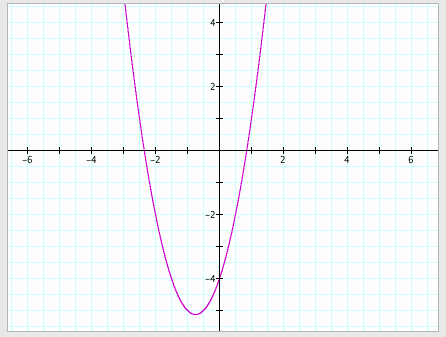
The vertex of this parabola can be found by completing the square.

 

Thus, the vertex is located in Quadrant III at the point (-3/4, -41/8).

Now, take the original equation and replace x with (x-4) and graph them both. Notice that the parabolas look exactly the same; the only difference (besides the color, of course) is that the function whose variable is (x-4) has shifted to the right four units.

 

 

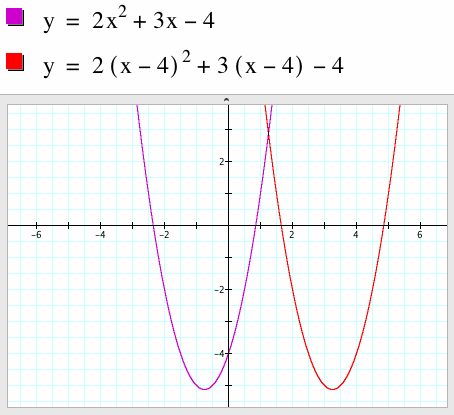
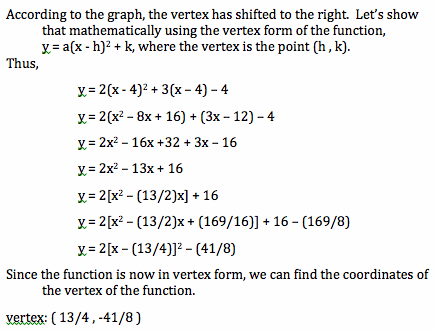
Thus, the vertex is now located in Quadrant 1 at the point (13/4, -41/8). Note that this point is 4 units to the right of the original vertex. Thus, changing the variable from x to (x-4) translated the vertex to the right 4 units. Futhermore, subtracting any constant h from the variable x will translate a point h units to the right.

Now, let's try to move both of these functions into Quadrant II by changing their equations.

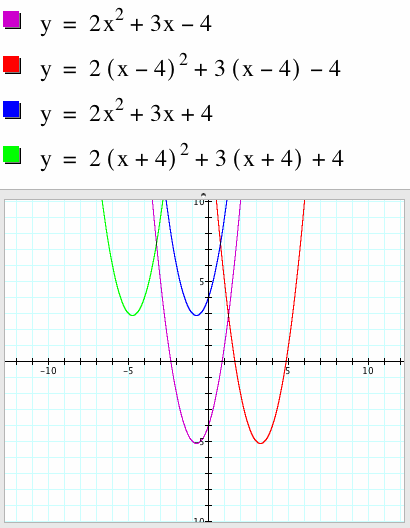
In the original parabola, changing the y-intercept from -4 to 4 will move the graph from Quadrant III to Quadrant II.

 

 

 

 

 

Thus, the translated vertex is at the point ( -3/4, 23/8).

However, making that change alone in the second parabola will not move the graph of the second parabola to Quadrant II; it will in fact move it to Quadrant I, as shown here.

Therefore, changing (x - 4) to (x + 4) as well as changing the y-intercept from -4 to 4 will move the graph of the second parabola to Quadrant II.

Hence, the translated vertex of the second parabola is now located in Quadrant II at the point (-19/4, 23/8). Thus, changing (x-4) to (x+4) translates the original parabola's vertex 4 units to the left; also, changing the y-intercept from -4 to 4 translate the vertex up 8 units. Thus, the original vertex (-3/4, -41/8) is translated by (-4, 8) to the new point (-19/4, 23/8), the vertex found in this problem.

Now that both parabolas are moved to Quadrant II, how can the equations be transformed in order to make the two functions concave down while keeping their vertices on the same points?

In order to transform a parabola from being concave up to concave down, look again at its vertex form.

In order to maintain the vertex of a parabola but reverse its concavity, make a negative. Thus, the vertex form of a parabola whose concavity is reversed is

Thus, to change the original parabola in Quadrant II from concave up to concave down, change the value of a from positive to negative. Then, simplify it to its standard form.

In the original parabola, a = 2.

 

 

 

 

 

 

Shown is the original function, the function translated to Quadrant II, and the function now concave down.

Similarly, making the value of a negative in the second parabola will make it concave down.

In the original (x - 4) parabola, a = 2.

 

 

 

 

 

 

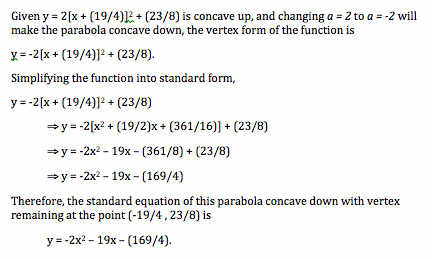
Shown is the original (x-4) function, the function translated to Quadrant II, and the translated function now concave down.

Thus, we have seen graphically how changing different values in the vertex formula of a parabola will translate, or move, the parabola. Given the vertex formula for a parabola,

with vertex (h, k), the following changes will transform the graph of a parabola.

 

 

Return