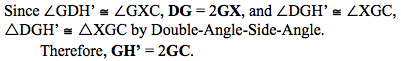Ratio of Segments on the Euler Line
by
Mike Rosonet
This page is devoted to proving that, for any triangle,
- the centroid, orthocenter, and circumcenter are collinear, and
- the distance between the centroid and the orthocenter is twice the distance between the centroid and the circumcenter.
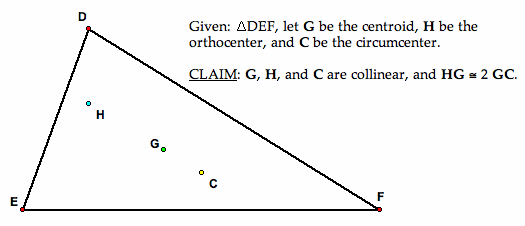
There are several special points in the center of a triangle, but focus on four of them: the centroid, the orthocenter, the circumcenter, and the incenter. Defining them first is necessary in order to see their relationship with each other.
The centroid (G) of a triangle is the point of intersection of the three medians of the triangle. A median is a segment constructed from a vertex to the midpoint of the subtending side of the triangle.
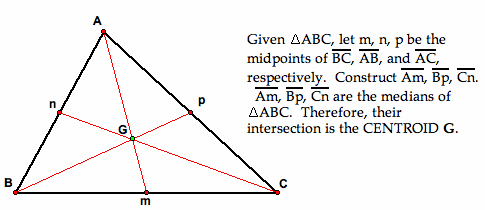
The centroid is located 2/3 of the way from the vertex to the midpoint of the opposite side.
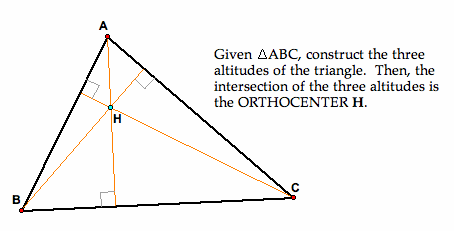
The orthocenter (H) of a triangle is the point of intersection of the three altitudes of the triangle. An altitude is a line constructed from a vertex to the subtending side of the triangle and is perpendicular to that side. It should be noted that the orthocenter, in different cases, may lie outside the triangle; in these cases, the altitudes extend beyond the sides of the triangle.
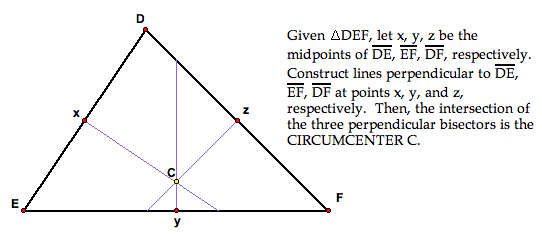
The circumcenter (C) of a triangle is the point of intersection of the three perpendicular bisectors of the triangle. A perpendicular bisector is a line constructed at the midpoint of a side of a triangle at a right angle to that side. It should be noted that the circumcenter, in different cases, may lie outside the triangle; in these cases, the perpendicular bisectors extend beyond the sides of the triangle.
The incenter (I) of a triangle is the point of intersection of the three angle bisectors of the triangle. An angle bisector is a line whose points are all equidistant from the two sides of the angle. Thus, the incenter (I) is equidistant from all three sides of the triangle.
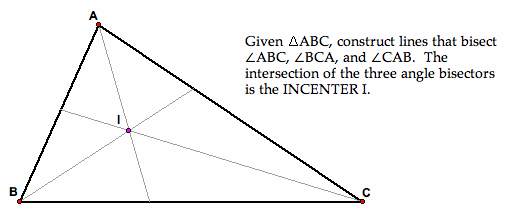
Now, we will prove that the centroid (G), the orthocenter (H) and the circumcenter (C) are collinear and that HG is congruent to 2GC.
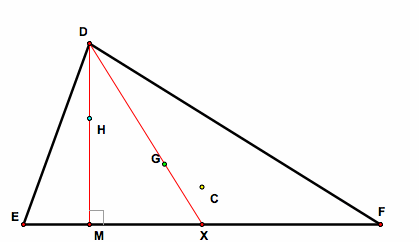
1. Let X be the midpoint of EF. Construct the median DX. Since G is the centroid, G is on DX by the definition of centroid. Also, construct the altitude DM. Since H is the orthocenter, H is on DM by the definition of orthocenter. Therefore, DM meets EF at a right angle.
2. Construct a line through points C and G so that it intersects DM. Note, it appears that line CG intersects DM at the point H. However, this has not been proven yet. So, label the point of intersection H'.
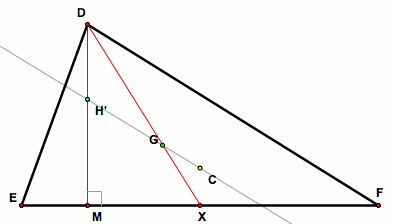
3. Construct CX. Since C is the circumcenter, CX meets EF at a right angle by the definition of circumcenter.
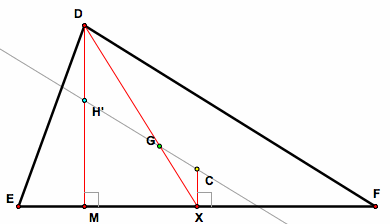
4. Since DM and CX both meet EF at right angles, DM is parallel to CX. Then, the median DX is a transversal that cuts DM and CX.
5.
6. Since G is the centroid, DG = (2/3)DX and GX = (1/3)DX. Therefore, DG = 2GX.
7.
8. Thus, H' is located at the intersection of DM and GC and is in fact on the line GC such that GH' = 2GC. Thus, G, H', and C are collinear. Similarly, H' can be proved to be located on the altitudes constructed from vertices E and F so that GH' = 2GC. Therefore, H' lies on all three altitudes.
9. Thus, H' is the orthocenter because it is lies on all three altitudes. Yet, by the given hypothesis, H is the orthocenter. Thus, H' = H.
10. Therefore, G, H, and C are collinear, and GH = 2GC.
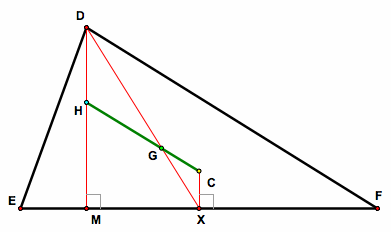
The line that connects the centroid (G), the orthocenter (H), and the circumcenter (C) is called the Euler Line.