Tangent Circles
by
Mike Rosonet
This investigation begins with the following problem:
Given two circles and a point on one of the circles, construct a circle tangent to the two circles with the given point as the point of tangency.
This investigation will use GSP to learn about a circle tangent to two other circles. Use this GSP file, if necessary.
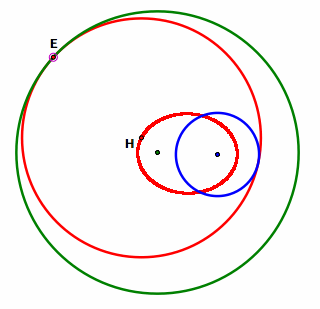
the red circle with center H is tangent to both the green circle and the blue circle
It is worth noting that the given GSP file will allow the investigator to look at other occurs of the circles. In this investigation, the one circle contains the other. A worthy extension would be to look at two circles that are completely disjoint, or are tangent at one point, or intersect at two different points.
What does the locus of the center H of the constructed red circle?
To investigate this, trace the point H as the point E revolves around the green circle. This will trace the locus of H.
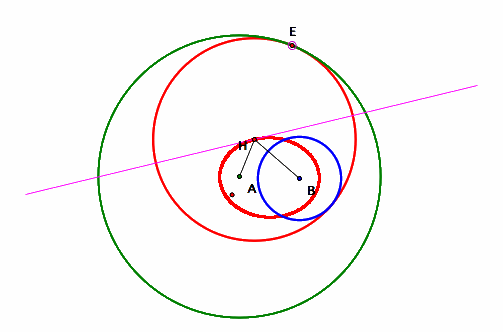
It looks like the locus of H is an ellipse. However, this needs to be proven. To do so, construct segments from H to the two centers of the green and blue circles. If the locus is an ellipse, then the sum of these two segments will remain constant as H revolves around its trace, and the centers of the green circle (F1) and blue circle (F2) are the foci of the ellipse.
Here is a GSP file to check that the sum remains constant as H revolves around its trace.
Therefore, the locus of H is indeed an ellipse.
Tangent to the ellipse at H
To continue this investigation, it's necessary to construct a line tangent to the ellipse at the point H.
To do this,
- Construct a line through H and F1.
- Construct a segment from H to F2. Then, construct a circle with center H and radius equal to the segment from H to F2. Lastly, construct the intersection I of the line through H and F1 and the constructed circle.
- Construct a segment from I to F2. Then, construct the midpoint M of the segment from I to F2.
- Finally, construct a line through H and M. This line is the tangent line to the ellipse through H. (For the sake of eluding confusion, hide all other elements except for the tangent line through H.)
image of the line tangent to the ellipse through point H
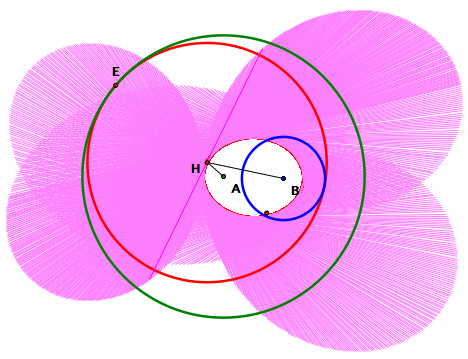
What does the envelope of the tangent line look like?
To complete this investigation, consider the envelope of the tangent line as H traces along the ellipse.
To construct the envelope, trace the tangent line and set the point E into motion. The resulting animation will give the envelope of the tangent line as the point H traces along the ellipse.
the envelope of the line tangent to the ellipse at the point H
Extension
What is the locus of the center of the circle tangent to the two given circles if the given circles are completely disjoint? What does the envelope of the tangent line to that locus look like?
What if the circles were tangent at one point, but one did not contain the other?
What if the circles intersected at two points?