Altitudes and the Orthocenter
by
Mike Rosonet
This exercise will compare the relationship between the altitudes and the orthocenter of a given triangle.
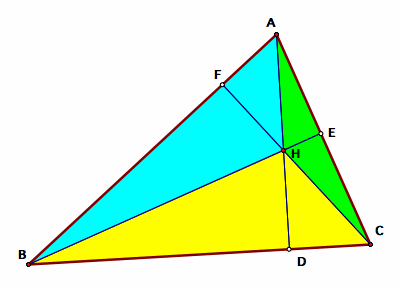
First, construct any acute triangle ABC. Then, construct the orthocenter H of triangle ABC. Let the feet of the altitudes from A, B, and C be D, E, and F, respectfully.
Prove (a)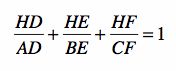 
and (b) 
.
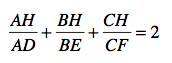Proof of (a).
1) First, consider the area of triangle ABC. Recall that the area of any triangle is the base multiplied by the altitude divided by two. However, in constructing the orthocenter of triangle ABC, three altitudes were constructed. Thus, there are three equivalent formulas for the area of triangle ABC.
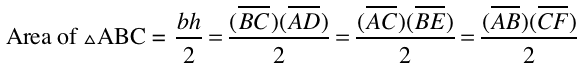
2) From the figure, it can be seen that ratios can be made between the three highlighted triangles (triangle HBC, triangle HCA, and triangle HAB) and triangle ABC.
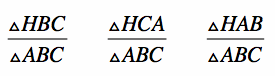
3) Now consider the areas of triangle HBC, triangle HCA, and triangle HAB.
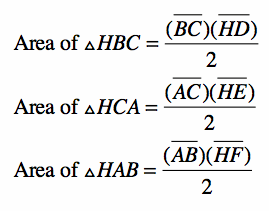
4) Since the sum of the areas of triangle HBC, triangle HCA, and triangle HAB equal the area of triangle ABC, the sum of the ratios of the areas of triangle HBC, triangle HCA, and triangle HAB over the area of triangle ABC equals 1, i.e.,
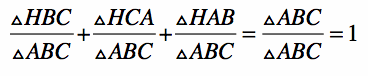
5) Substitute the formulas for area derived in steps 1 and 3 into the equation in step 4, and simplify.
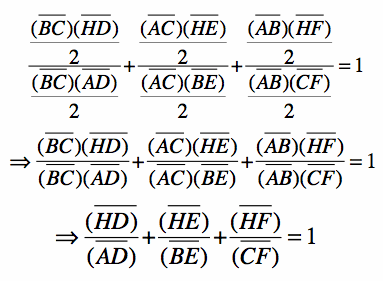
6) Thus, the sum of the ratios of the altitudes of the shaded triangles over the corresponding altitudes of triangle ABC equals 1.
Proof of (b).
1) Since the whole is equal to the sum of its parts,
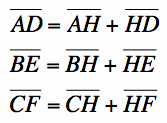
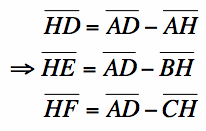
2) Solve for the altitudes of the three interior triangles, as shown above. From this, using the ending equation in step 5 of part (a) and substituting the above equations,
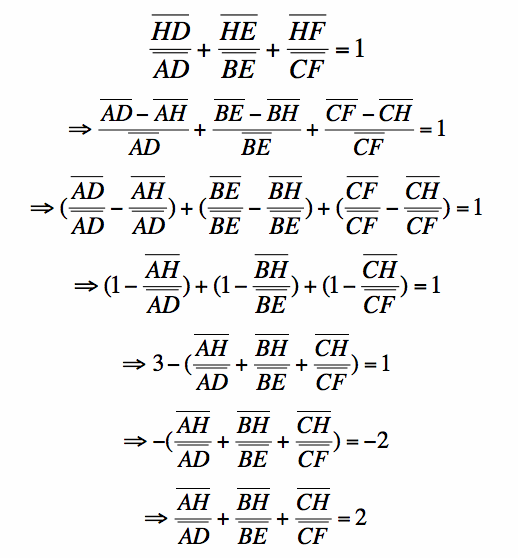
3) Thus, the sum of the ratios of the altitudes of the interior triangles over the altitudes of triangle ABC equals 1, and the sum of the ratios of the segments from the vertices of triangle ABC to the orthocenter H over the altitudes of triangle ABC equals 2, thereby proving parts (a) and (b).
This exercise looks at the relationship between the altitudes and the orthocenter of an acute triangle. Through algebra, the ratios and sums in parts (a) and (b) were proven true.
Do these sums hold true in an obtuse triangle?
What about in a right triangle?