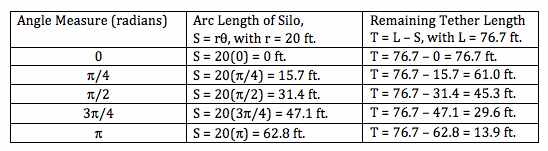Grazing Area
by
Mike Rosonet
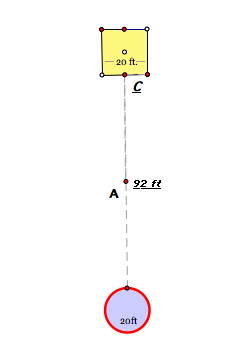
Farmer Jones had a goat on a tether. He tied the end of the tether not attached to the goat to a line that connected two structures in a field.
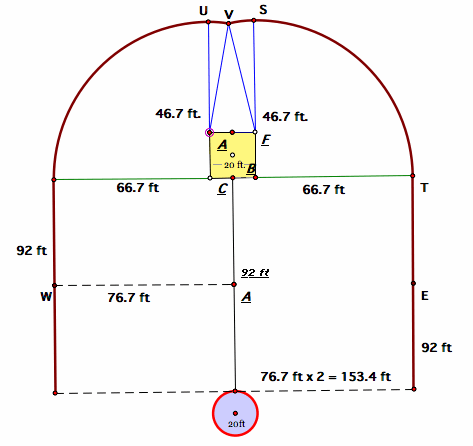
One structure is a square 20' by 20' shed.
The other structure is a silo that is 20' in diameter.
The length of the line connecting the shed to the silo is 92 ft. From the center of the shed to the center of the silo, the distance is 112 ft.
The tether for the goat is 76.7 feet long. The tether is tied somewhere along the line connecting the shed to the silo.
Explore the area over which the goat can graze as the tether is moved along the line connecting the shed to the silo.
There are multiple ways in which to interpret this problem. One such way is to find the total possible area of the field upon which the goat can graze. This is the approach used in this investigation.
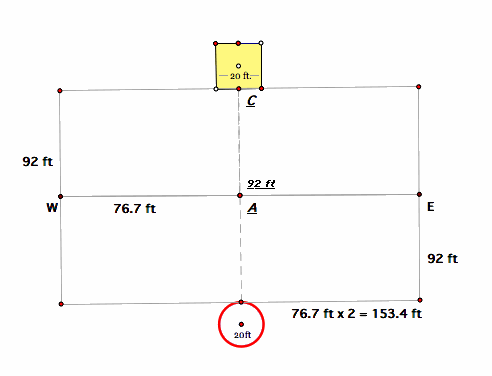
An image of the field with all initial measurements
It is helpful to look at the field in sections. The sections will be the rectangular area of the field between the shed and the silo, the area beside and behind the shed, and the area around the silo.
One place that the goat could be tethered is at the midpoint of the line connecting the shed and silThe easiest section in which to begin this investigation is the rectangular area of the field between the shed and the silo.
Because the tether is 76.7 feet long, multiplying that length by 2 will give the distance possible for the goat to travel along a line perpendicular to the line connecting the structures, a length equal to 153.4 feet. Thus, the dimensions of the rectangular section of the field are 92 ft by 153.4 ft. Using the formula for the area of a rectangle, A = lw, the area of this rectangular section is 14,112.8 sq. feet.
Now, consider the area near the silo.
If the goat's tether were at the point where the line connecting the shed to the silo connects to the silo, then the goat would have a somewhat circular region to graze in. However, the silo itself is in the way of the goat's grazing. Thus, looking at the length of the silo from the point that the line connecting the silo to the shed to specific points on the silo is best to estimate the goat's grazing area.
The diagram shows tangent lines at angle measures 0°, 45°, 90°, 135°, and 180°. If an arc were constructed along the endpoints, this would give a visual of the goat's grazing area to the left of the silo. Similarly, this image could be reflected across the diameter drawn from point G through the center of the silo to show the same arc containing the goat's grazing area to the right of the silo.
Using the formula for arc length, which is
, at the given angle measures, it is possible to find the length of the silo from the point that the line connecting the shed to the silo to the point on the silo at those angles. It is also possible to determine how much tether is left over by subtract the arc length from the tether, which is shown as the extended pink segments in the diagram.
Estimating the area formed by these two arcs and the silo can be completed through the use of triangles. By using the four lesser tether values, an underestimation for the area can be made. Likewise, by using the four greater tether values, an overestimation for the area can be made. Then, find the average of the 2 estimates to find the best approximation for the grazing area around the silo.
This table reveals the length of the silo from the point that the line connecting the structures to the point at each of the given angle measures as well as the remaining length of the goat's tether.
Underestimate of the area =
= 2687.0 sq. ft.
Overestimate of the area =
= 4921.4 sq. ft.
Best approximation = 2
= 7, 608.4 sq. feet.
Lastly, consider the area of the field around the shed.
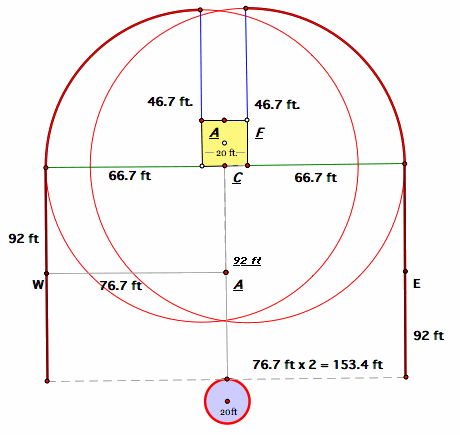
To begin this investigation, construct a circle whose center is one of the bottom corners of the shed and whose radius is the remaining length of the tether as shown below in green.
If the point C is the midpoint of the front-facing wall of the shed, then the distance from the point C and the corner of the shed is 10 feet. If the goat's tether is at point C, then 10 feet of the tether runs parallel to the wall of the shed. Thus, there is 66.7 feet of tether remaining. This length is the radius of the constructed circles.
Now, only 1/4 of each circle is needed in this investigation. The area of the lower halves of the circles have already been counted in the area of the rectangular region. The top-right sector of the left-hand circle intersects with the top-left sector of the right-hand circle. (The region between the two blue segments will be accounted for shortly.) Thus, it is sufficient to find the area of the top-left sector of the circle on the left and multiply that area by 2 to find the area of the two sectors of the red circles. To do this, use the formula for the area of a sector of a circle:
.
Because the shed has corners at ninety-degree angles, the measure of the theta for both of these sectors is 90°. However, this value must be converted to radians in order to evaluate the area using the formula. Also, the radius r = 66.7 feet. Hence, the area of the two sectors as shown above between the blue and green segments is approximately 6988.3 sq. feet.
Now, construct circles whose centers are the top two corners and whose radii equal the blue segments, which are 46.7 feet long. It is necessary to only find the point where the two circles intersect between the two blue segments and find the area of those small sectors. Once that point is found, for the sake of simplification, construct arcs between the points on the circles at the end of the radii and the intersection point; it is not necessary to maintain the rest of the circle as the area of those regions have already been accounted for.
Construct segments from the corners of the shed to the intersection point V (as shown in the diagram). These segments are also 46.7 feet in length because they are constructed from the center to the circumference of the circles.
Again, use the formula for the area of a sector. Unfortunately, there is no simple way to find the measure of the angles of these two sectors. If the investigator is using a software program, use the "measure" function; if the investigator is using a compass and straightedge, use a protractor to find the measure of the angle. If human error causes the angle measures to be different, find their average as this point in the investigation is based on estimation.
Hence, using the formula for the area of a sector, r = 46.7, and the angle measure in degrees is 11.81° (which must be converted to radians), the area of the two sectors between the two blue segments (not including the blue triangle) is approximately 449.5 sq. feet.
Lastly, to find the area of the blue triangle, use Heron's Formula:
. Let the blue segments be a and b, and let the side of the shed be c. Thus, s = 56.7 and the area of the triangle is 204.0 sq. feet.
Thus, the area of the region around the shed is 7641.8 sq. feet.
Therefore,
the best approximation for the goat's total grazing area is the sum of the areas of the regions.
Hence,
Total area = 14,112.8 sq. ft.+ 7608.4 sq. ft.+ 7641.8 sq. ft. = 29, 363 sq. feet