Goat Time

By

Brandon Samples

Farmer Jones had a goat on a tether. He tied the end of the tether not attached to the goat to a stake in a field. Over what area could the goat graze?

There are two structures in the field:

-- a shed that is 20 ft long and 20 feet wide (square)

-- a silo that is 20 ft in diameter

The center of the shed and the center of the silo are on a line and the distance apart is 92 feet. The distance from center to center, if you wanted to use this data, is 112 feet.

The tether for the goat is 76.7 feet long. The stake to which the tether is tied is somewhere along the line of centers between the shed and the silo.

Explore the area over which the goat can graze as the stake is moved along this line segment from the midpoint of the side of the shed to the edge of the silo.

Silo

First, let's explore the area that the goat can graze around the back on the silo. Let's consider the following diagram.

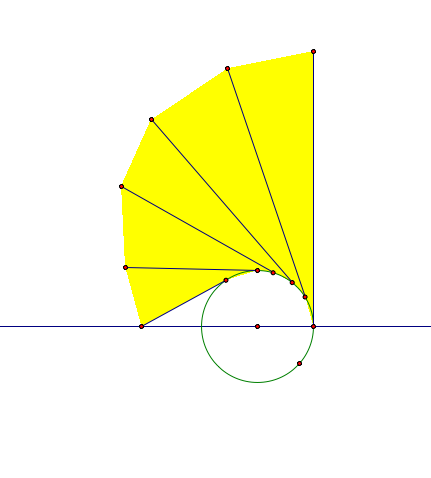
The polygonal region above indicates the method that we would want to use to approximate part of the area around the back of the silo. We know that doing these slices indicates that we should be computing definite integrals. In order to do so, we need to know where the tether hits the horizontal line through the center of the circle. We can use mathematica to approximate. The tangent line through any point on the circle is given by y = -cot(theta)(x-10cos(theta))+10sin(theta), so the intersection with the hortizontal line occurs when x = 10sin(theta)tan(theta) + 10 cos(theta). Now, the angle for which the tether hits this line is exactly the point such that the distance between the points

(10sin(theta)tan(theta)+10cos(theta),0)

and

(10cos(theta), 10sin(theta))

is equal to the length of the tether.

Let's estimate this using mathematica:

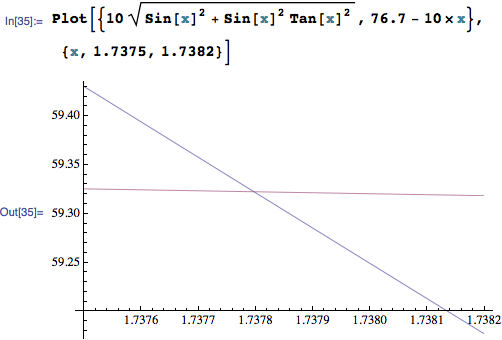
Now, we know that the distance between those two points must equal to the length of the tether, which is obtained by subtracting the arclength from the total length.

It appears that a good estimate occurs for theta approximately 1.7378 radians.

Next, we want to compute the area swept out by the goat around the back of the silo. The area represented by the yellow sector is approximated by the following definite integral.

Now, let's approximate the area between the horizontal and the tether to the left of the silo.

Using the following two triangles, we can estimate the total area:

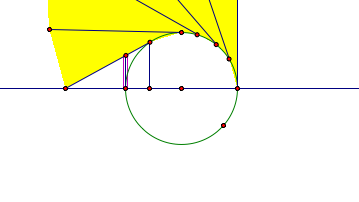
The smaller triangle has base length of 50.1582 and the larger triangle has base length 60.1582. Then since the height of the larger triangle is 9.86087, we can use similar triangles to compute the height of the smaller triangle to be 8.22171. Therefore, the smaller triangle has area 206.193 and the larger triangle has an area of 296.606. Obviously the actual answer lies between these two values and seems to be less than half, so we can take 240 as our estimate.

Finally since this represents half of the area behind the silo, we get a total estimate of 3213.75 x 2 + 240 x 2 = 6907.5.

Middle of the Field

Now the middle of the field has a length of 92 feet and a length of twice the length of the tether (76.7 feet), so the field in the middle has a length of 14112.8 sq feet.

Barn

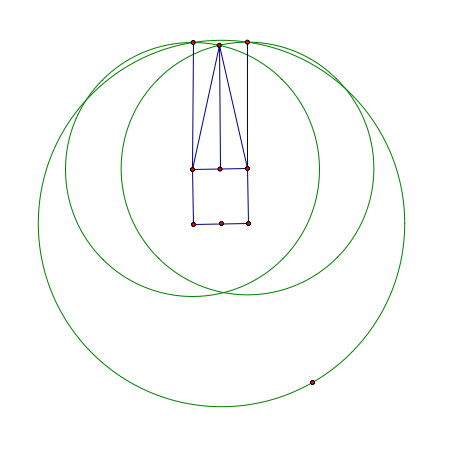
The above area can be estimated by the two outer sectors and the two inner triangles. Let's start with the sectors. The sector has a radius of length 46.7 and an angle of .215806, so the total area is 1/2(46.7)^2(.215806) = 235.325. Since there are two of them, we have an area of 470.649. Next, the triangle has a base length of 10 and a height of 45.6168, so the area of the triangle is 1/2(10)(45.6168) = 228.084. Again, since there are two of them, we have an area of 456.168.

Finally, we need to compute the area for the portion of two circle to the left and right of the barn.

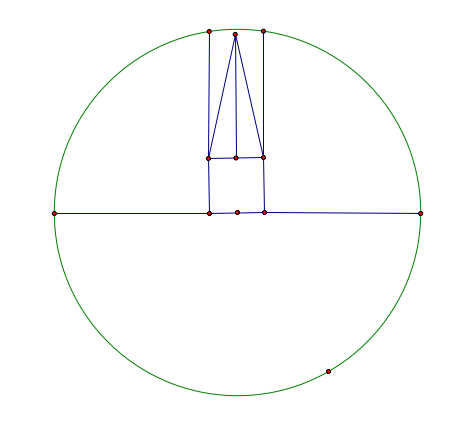
They are circles with radius 66.7, so the two area of one sector is 1/2(66.7)^2(pi/2) = 3494.15, hence two sectors yields 6988.3.

Conclusion