
A
&O
By Brandie Thrasher
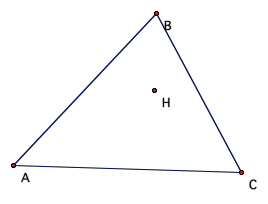
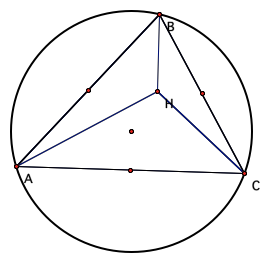
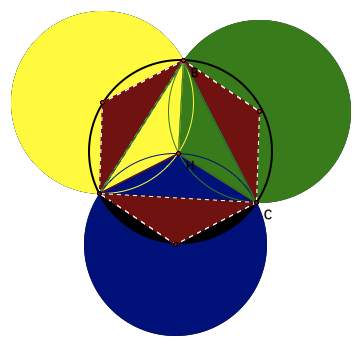
LetŐs investigate altitudes and orthocenters, and begin with triangle ABC with its
constructed orthocenter H.
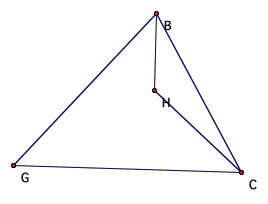
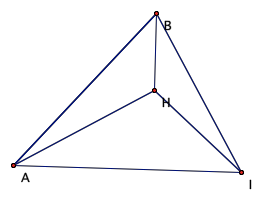
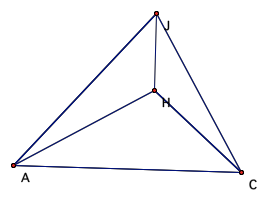
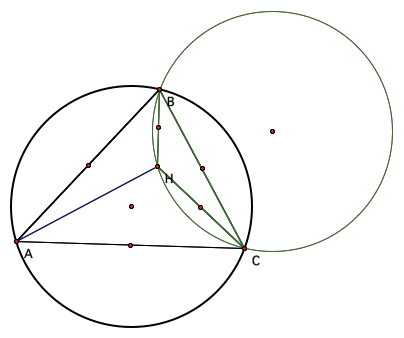
Now, lets contsrtuct the
orthocenter for triangle HBC (labeled G), Followed by the orthocenter of
triangles HAB (labeled I), and HAC (labeled J)
Now we will construct the circumcircles
of triangles ABC, HBC, HAB and HAC
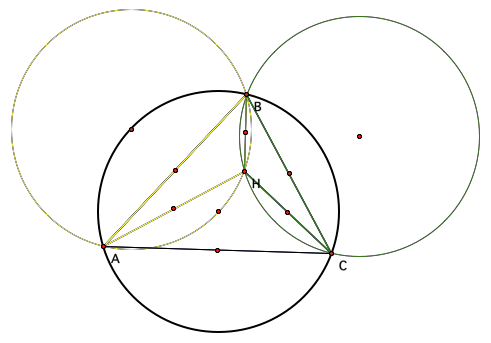
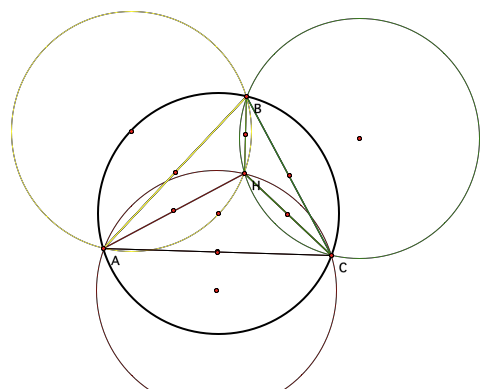
Once the construction is complete, our
orthocenterŐs and circumcircles made a beautiful
display
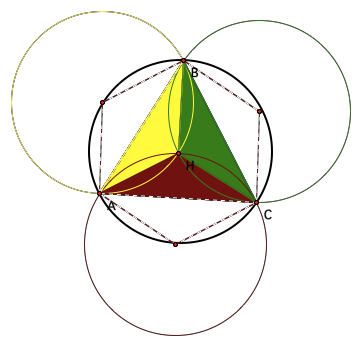
But what exactly do we have? Lets construct
some conjectures:
1.
The radii of
the circumcircles constructed from triangle ABC form
a hexagon.
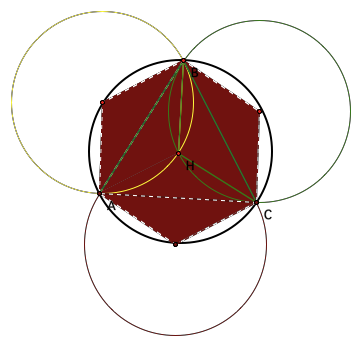
2.
These same radii form three triangles
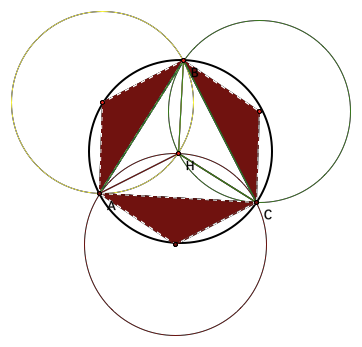
3.
The three
newly formed triangles are similar to triangles HAB, HBC, and HAC.
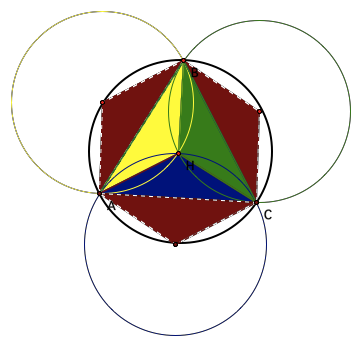
4.
The area of
all four circles is congruent
Students can take these conjectures and turn
these into proofs, investigating the many interesting ways altitudes and orthocenterŐs affect one another.