Explorations

By Brandie Thrasher

It is true that for an equilateral triangle, its triangle of medians is also equilateral. What about an isosceles triangle? Will its triangle of medians also be isosceles? Lets explore!

First, lets answer the question, what is a triangle of medians?

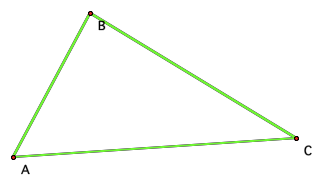
Ok, well given this triangle

Construct the medians (a segment joining a midpoint of a leg to an opposite vertices)

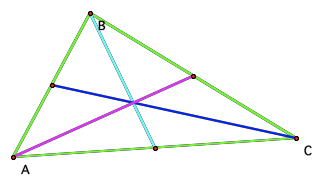
From the these segments, we create a triangle with sides of equal length of these medians

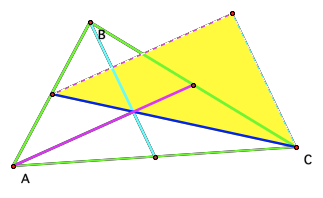
The triangle shown with the yellow interior is the triangle of medians for triangle ABC.

Now, given an isosceles triangle (JFI) let’s construct its triangle of medians ∆LHI

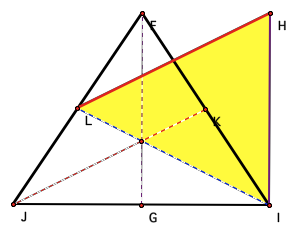
Since ∆JFI is isosceles having line segments JF and IF being congruent to one another, there medians must also be equal, thus segments LI and KJ are congruent to one another. In our triangle of medians, segment LH represents segments segment JK, which is congruent to segment LI, thus our triangle of medians is also isosceles with base IH.

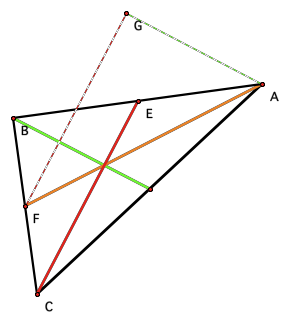
What about other special triangles? Will a right triangle generate a right triangle of medians?

Here is a right triangle with its median of triangle constructed

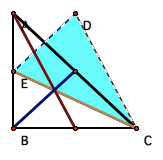
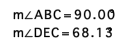
As shown, ∆ABC is in fact a right triangle, but the triangle of medians (∆DEC) is not a right triangle. It is in fact a scalene triangle

Will this always be the result?

Here is a right isosceles triangle, and its triangle of medians is isosceles, but not containing a right angle.

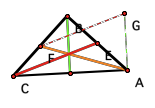
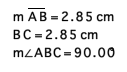
But, as our triangle expands where angle BAC approaches 35.2˚ and angle 54.75˚ angle FGA of our triangle of medians approaches and exceeds 90˚, thus there is a point in which a right triangle produces a right triangle of medians.

return