More Quadratics!

by Brandie Thrasher

We have looked at a type of quadratic equation earlier (involving parabolas), and now we will be looking at graphs in the “xb” plane.

Lets look at the graph of x² +bx +1 =0

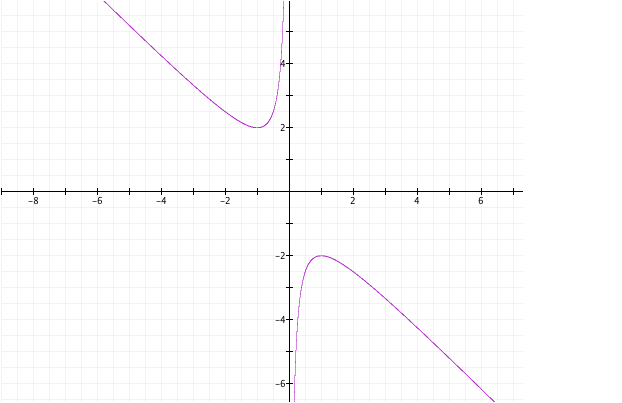
From our previous explanation of a parabola, we can see that this graph does not exactly fit our normal definition or view of what they are suppose to look like, nor is there only one graph present, but this IS a quadratic equation (where the highest power is 2). So what is an “xb” plane?

Most of us are only use to hearing about the “xy” or “xyz” plane.

Well, if we look at an ordered pair in the xb plane, it would be of the form (x, b) where our b is in they place of y. Thus from our equation x²+bx+1=0, (when solving for b)

b = (-x² – 1)/ x

This being stated, where x = 0 the graph is undefined, so the y-axis serves as an asymptote for our graph.

If we want to know the roots for our graph, we set b = to any number. Lets try

b=3

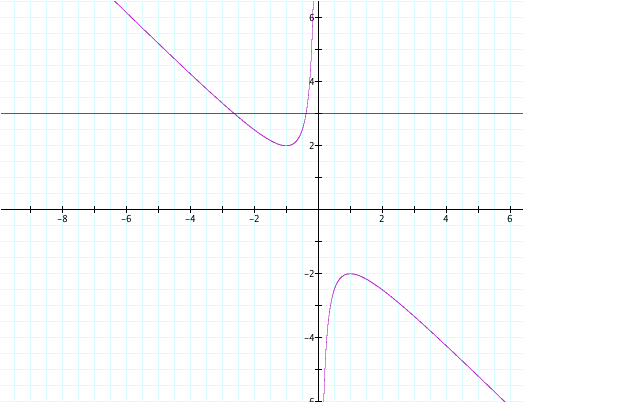
Our new graph (in red) shows that there are two real roots where b = 3.

Lets see what will happen to our graph when c = -1, or

b = (-x² + 1)/ x

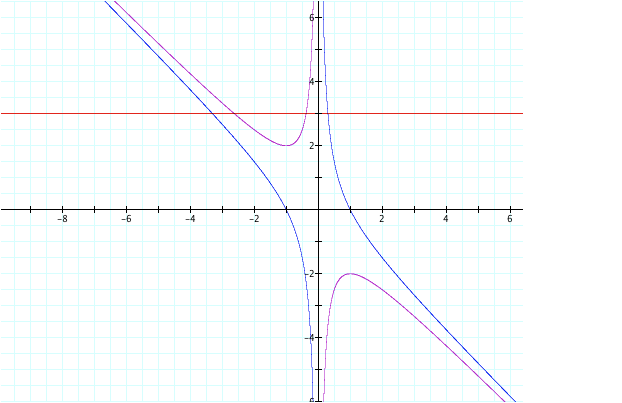
Our graph looks very different from the original, just by changing the sign of c, but it also uses the y-axis as a vertical asymptote. We can also see that at b = 3 there are still two real zeros.

Will the graphs take the same effect if we increase or decrease the values of c?

Let’s first try c = 3

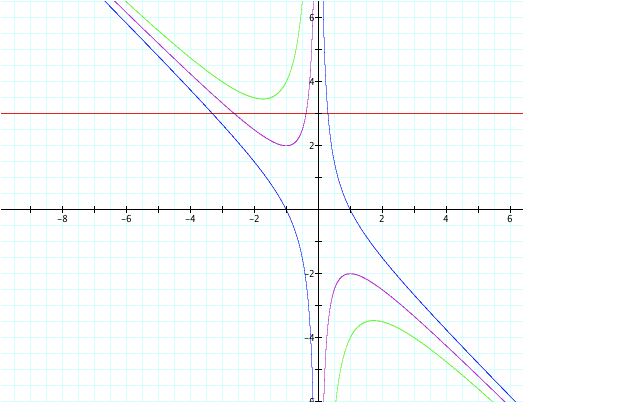
Now, lets try c = -3

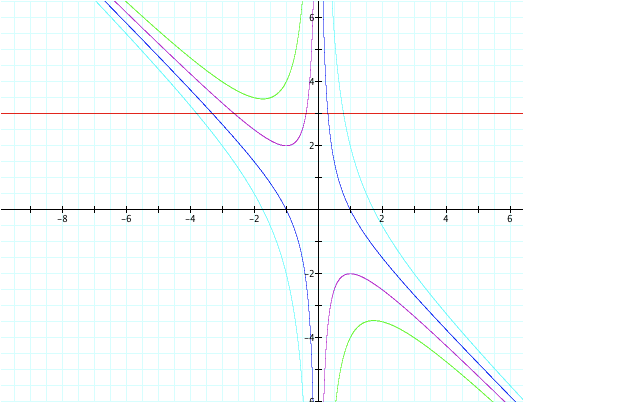
Our pattern holds true; where our graphs keep the same shape, but shift acordingly.

Now, lets take a look at a different equation,

2x + b = 0.

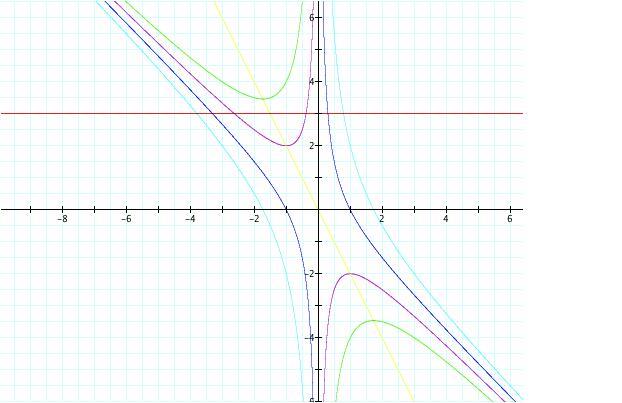
It appears that our equation cuts through each graph where c is positive. Actually the graph 2x + b = 0 is the first derivative of our original quadratic equation of x² + bx + c = 0. But we are still considering our graph in the xb plane, thus here b = -2x. It appears that or equation goes through the vertex of each graph.