Parametric Explorations

By: Brandie Thrasher

Wolframmathworld.com describes parametric equations as “a set of equations that express a set of quantities as explicit functions of a number of independent variables, known as ‘parameters’.” An example of this type of equation set can yield the graph of a circle.

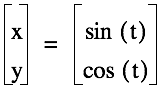
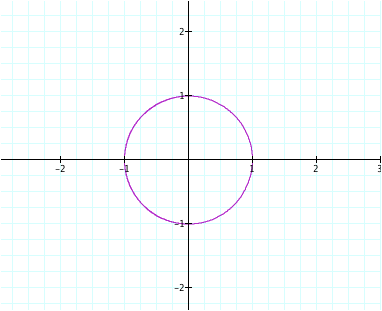
The parameter (or quantity that defines the system and its characteristics) is usually expressed with the variable t. We will be using t where 0 < t < 2p.

When we introduce a and b into our equation, our graph begins to take shape, as long as a and b are not equal.

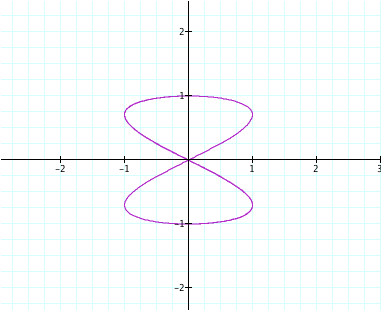
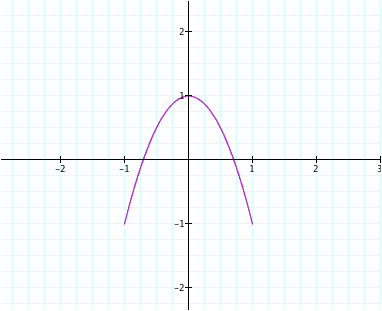
Here, a = 2 and b = 1

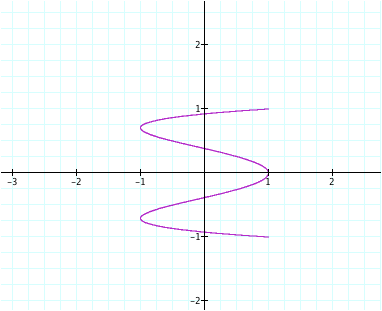
Here, a = 1 and b = 2

If we change our definitions (swapping) x and y, our graphs shift.

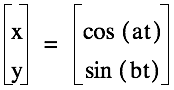
here, a = 1 and b=2 then the second graph has a = 2 and b = 1

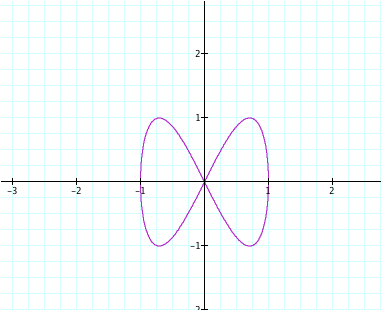
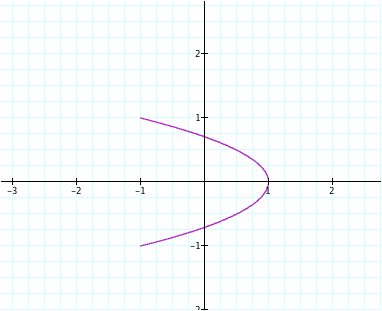
It appears that our line of symmetry is dependent on what parameter is set to x. In our first set, x was equal to the sin function, yielding a graph with a line of symmetry at q = ^p/₂ while x that is set equal to the cos function yields a line of symmetry at q = 2p.

With our first set, if we leave b =1, our graphs shows the amount of loops, represented by the value of a. here is a = 3, 4, and 5

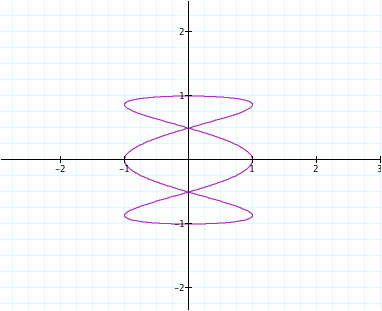
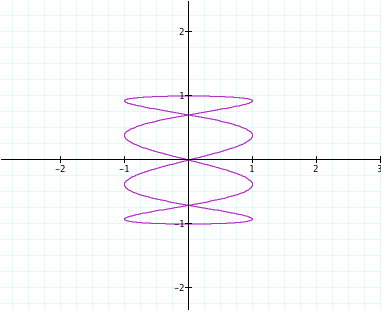
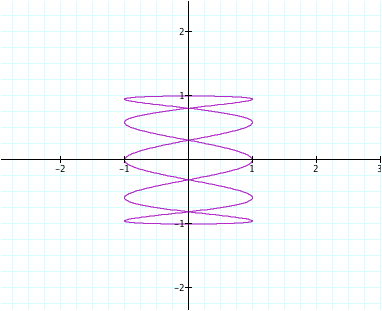
If we change a from the second set to the same values, we would actually receive the same graphs for the odd values, but a = 4 would display

Return.