
Tangent Circles
BY: BRANDIE THRASHER
We are given the task to construct a circle that is
tangent to two circles, given a point, in which that particular point is along
the line of tangency to the circles.
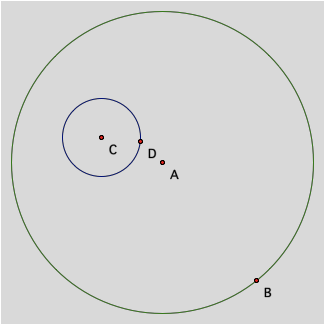
We begin by constructing a circle

We then construct another circle (in this case
inscribed in the larger circle)
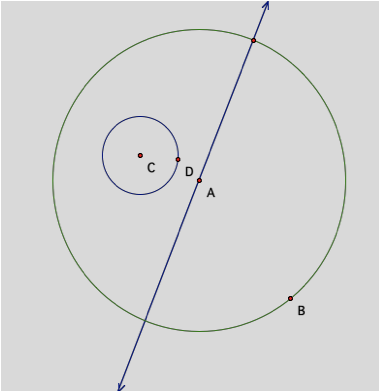
Next, we construct a point on the outside circle and
construct a line segment from the point to the center of circle A
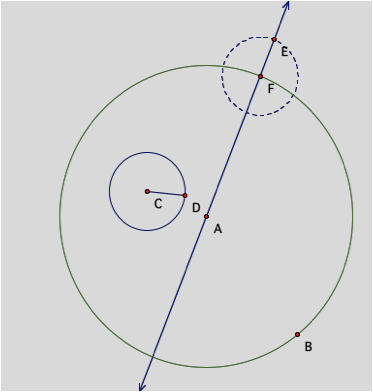
We then construct a circle congruent to circle c
centered at our point (F) created on circle A.
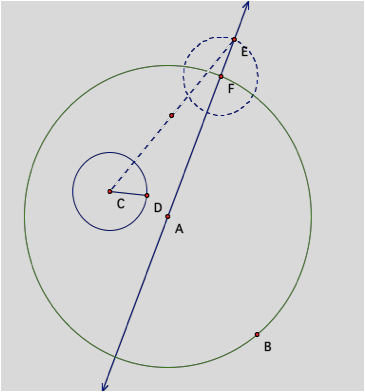
We now create a segment between points C and E and
find its midpoint
Next, we will create perpendicular line to go through
midpoint G. The point at which this line intersects line FA, will be labeled as
H
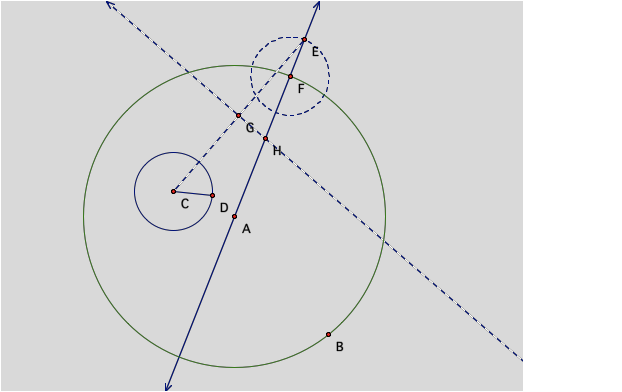
From this construction, we will make a new circle with
center H and point F. This circle will be the circle tangent to both circle A
and C.
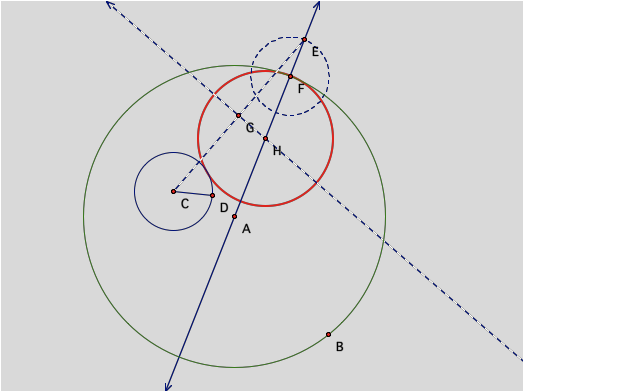
Here it is, all cleaned up!
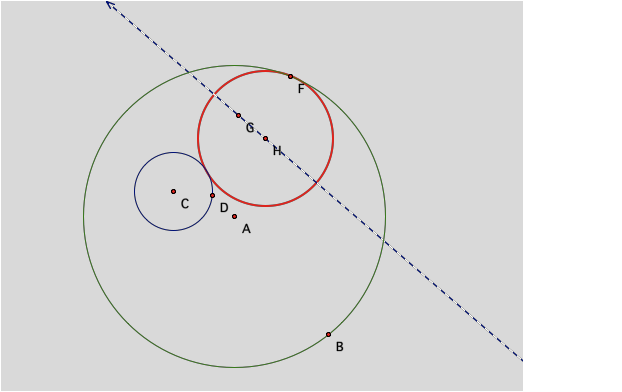
When the given point is traced alongside the
perpendicular line, another object is formed:
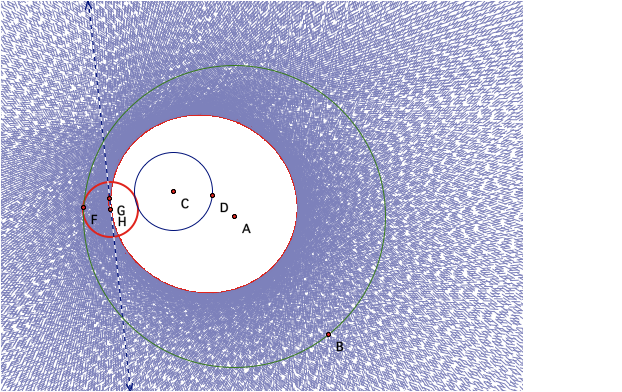
What are some conjectures we can come up with that can
interpret what is happening?
Would we get the same resut if our tangent circle was not inscribed in the bigger circle?
Investigate more!
See the animation and script
tool here