The Quadratic Weight-Loss Gene
by Patty Wagner
As women all over America desperately search for the perfect weight-loss stimulant, the quadratic equation has silently gone about employing its own, not-so-secret, girth predicting factor. Hidden within the "genetic make-up" of every equation is a simple element that alone determines the pudge factor of the equation. For centuries, these equations have been manipulating this element to create a more svelte or buxom profile in the x-y plane. This manipulation does not occur without side-effects however; quadratic equations can experience frustrating "vertex shifting" as well as a very embarrassing "invertion" side effect.
To fully understand this phenomenon, we must look closely at the quadratic equation and the effect the manipulation of this "fat gene" has on its apparent shape.
Quadratic equations can be described in the x-y plane as y = ax2 + bx + c, where a, b, and c are the unique representations of each quadratic equation -- the equivalent of human DNA. It is amazing that so many apparently different quadratic shapes can be created from so few variables; but one needs only to remind oneself that there are an infinite number of possible values for each of these three variables; while for the remarkably diverse human race there are only 4.
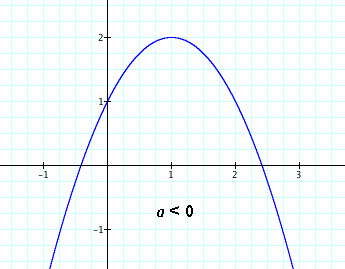
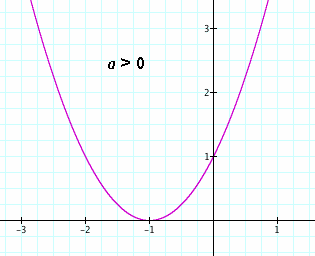
The standard quadratic equation can be divided into two types, somewhat like human gender. There is the upward opening and the downward opening. This characteristic is dependent on a. If a > 0, then the shape points upwards. If a < 0, then it points downwards. Of course, a can equal zero. We will reserve examination of this case for later.
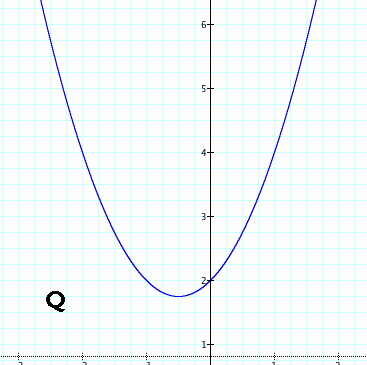
Let's examine one quadratic equation which has kindly agreed to manipulation for our further study.
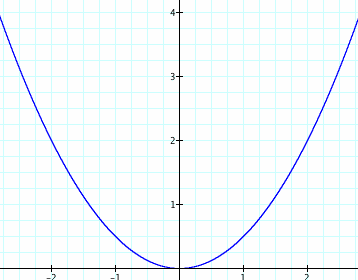
For privacy purposes, we will refer to this quadratic equation as "Q." Q has the values of a = 1, b = 1, and c = 2. As you can see, Q is a fairly standard form of quadratic: y = x2 + x + 2. It points upward (since a > 0), has the smooth curving shape of all quadratics, crosses the y-axis at y = 2, and enjoys a respectable vertex of (-1/2, 7/4). It is easy to see why Q crosses the y-axis at 2. Since its c value is 2, then when x = 0, y will always equal 2. This will never change, regardless of the values Q may substitute for a and b.
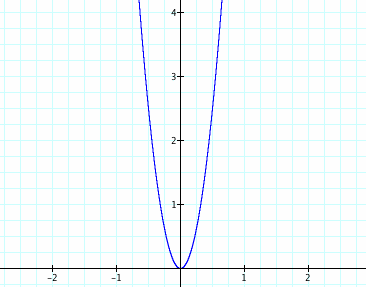
As we suggested earlier, Q is able to adjust its size through the manipulation of just one of its elements. That element is a. If we make just a small adjustment to this value, we immediately see its impact:
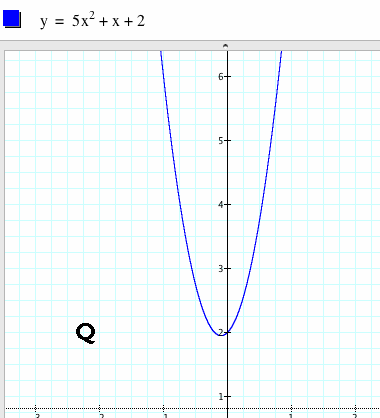
By simply changing a from 1 to 5, Q has lost a few dress sizes. It may be tempting at this point to say that Q has changed its "shape." And indeed, on the surface it seems that it has. However, this a manipulation is really all smoke and mirrors. If we zoom in on Q, we make a remarkable discovery. Q's shape has not changed at all, but rather appears to be different as long as the perspective stays the same. Here is a close up view of Q:
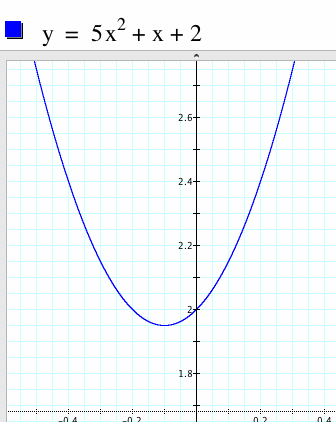
Surprisingly, this close-up view of Q allows us to see that Q is still the same shape it started with. However, we and (more importantly to Q) other quadratics, must "zoom in" to realize this. As quadratics don't tend to shift their perspectives regularly, they can be tricked into thinking that Q actually looks different. This is not so different from our human tendency to assume that a person is "standing still" although we know that in reality that same person is actually undergoing the equivalent of a high-velocity teacup ride by spinning around on the earth while it whizzes around the sun.
Although Q's shape may not have changed in reality, its position definitely has. Notice that Q has suffered the side effect that is standard for all quadratic equations in which b ≠ 0. We call this side effect "vertex shifting."
We can explore this side effect by dissecting the general form of the quadratic equation.
y = ax2 + bx + c = a[x2 + (b/a)x] + c
y = a[x2 + (b/a)x + b2/4a2] + (c - b2/4a) = a(x + b/2a)2 + (c - b2/4a)
Now that we have the general equation in vertex form, we can examine the vertex. Recall that the vertex of an equation of the form y = a(x - h)2 + k is (h,k). Therefore, our vertex is:
(-b/2a , c - (b2/4a))
Now we can see the source of the "vertex shifting." In quadratics that have a b value other than 0, the x-coordinate is determined by a ratio between a and b; likewise for the y-coordinate. In fact, we find we can predict the direction and amount of anticipated shift from changing the a value. A quadratic's propensity to suffer from vertical shift is directly associated with its b value.
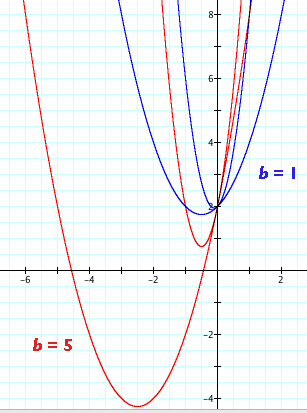
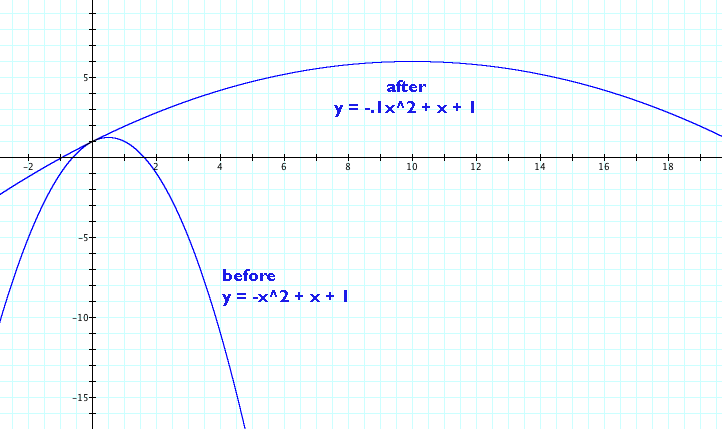
If we compare the shift experienced by Q (b =1), with that of R (b = 5), we can more easily comprehend this phenomenon. R (depicted in red in the graph) has an original equation of y = x2 + 5x + 2. As you can see, the only difference between R and Q is their b values.
When Q was changed from y = x2 + x + 2 into y = 5x2 + x + 2, its original vertex of (-½ , 7/4) shifted to (-1/10 , 39/20). This is a linear distance of √(1/2 - 1/10)2 + (7/4 - 39/20)2 = √1/5 ≅ .448 units.
R, on the other hand, in going from y = x2 + 5x + 2 to y = 5x2 + 5x + 2 experiences a shift from an original vertex of (-5/2 , -17/4) to (-1/2 , 3/4) which is a linear distance of √(5/2 - 1/2)2 + (-17/4 - 3/4)2 = √7 ≅ 2.65 units.
If we evaluate our general equation for vertex we can understand why this happens. First, if we look at the x-coordinate of the vertex, -b/2a, and fix a, we see that as the absolute value of b increases, the x-coordinate of the vertex gets further and further away from the origin. Looking at the y-coordinate of the vertex, c - b2/4a, and again fixing a, we see that as the absolute value of b increases the y-coordinate gets further and further away from c.
This is perhaps bad news for quadratics with large b values, but the good news is that the direction of vertex shift can also be predicted. If we again look at our x-coordinate for vertex but this time fix b, we see that as we increase the absolute value of a, our x-coordinate will get closer and closer to zero. Conversely, as we let the absolute value of a get smaller, we see that the absolute value of x will get further and further away from zero.
Switching to the y-coordinate of the vertex and fixing b, we see that as a gets larger we'll get closer and closer to c since c - b2/∞ takes us closer and closer to c - 0. On the other hand, decreasing a get us closer to c - ∞, thus the absolute value of y gets larger as a decreases.
Putting our findings for the x-coordinate and y-coordinate together, we see that as ∣a∣ gets smaller, our vertex gets further away from the origin. As ∣a∣ gets larger, our vertex gets closer and closer to (0,c).
Therefore, quadratics with large values of b just need to be aware that vertex shifting will be more dramatic when their a value is changed but if they are not unhappy with the location of their own (0,c), they can safely increase their values of a.
Decreasing a presents its own set of challenges. One may think that quadratics would rarely see the need to decrease their values of a. This is generally true for one class of quadratic; however, this type of quadratic equation occasionally attempts to create a more buxom profile in preparation for a Friday night out or, in rare cases, as a concession to a persistent quadratic partner. Of course, the other class of quadratic equation (similar to our male gender) is typically consumed with trying to increase their size as much as possible. To create this more substantial look, the quadratic must set its a value to 0 < a < 1. Here are some examples of quadratics that have undergone this procedure:
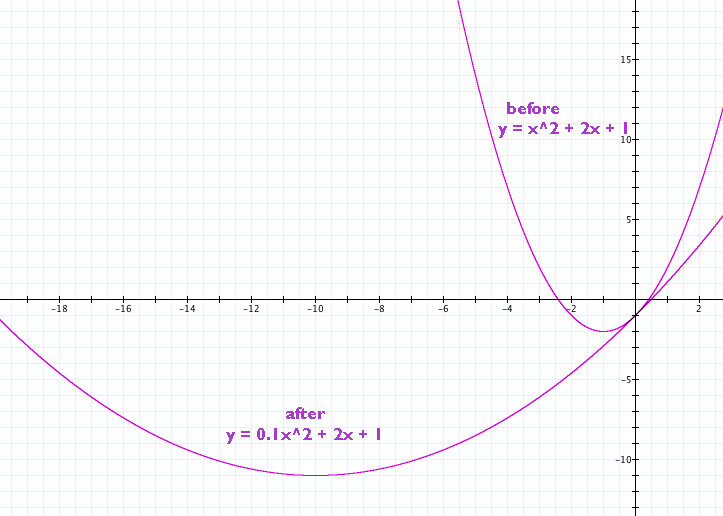
There is a particular danger for quadratics who let their a values approach zero. If they overshoot, and actually reach zero, they become the reviled "straight line." Here is an example of just such a quadratic equation that has slipped into being linear:
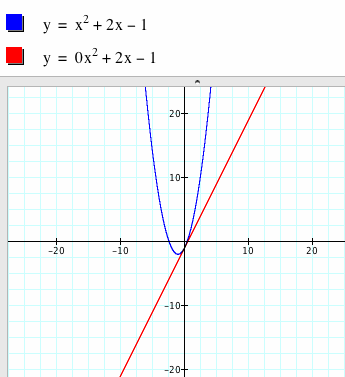
This quadratic equation started with an a value = 1. As you can see, when a became zero, the equation y = x2 + 2x - 1 became y = 0x2 + 2x - 1 which simplifies to y = 2x -1. This is the equation of a line with a y-intercept of -1 and slope of 2. Of course, quadratics have always accused linear equations of being very one-dimensional, fueling the animosity that exists between the two. And truthfully, although linears and quadratics are closely related, they are entirely different species, which explains the forbidden nature of letting one's a value go to zero.
Although the accidental slippage into linear equation is a faux pas in the quadratic world, it is social suicide to actually go past zero and slip into the opposite sign for a. This produces the dreaded "invertion." Here is a picture of a quadratic that was captured by hidden video accidentally pushing their a value too far in the presence of a quadratic it was trying to impress.
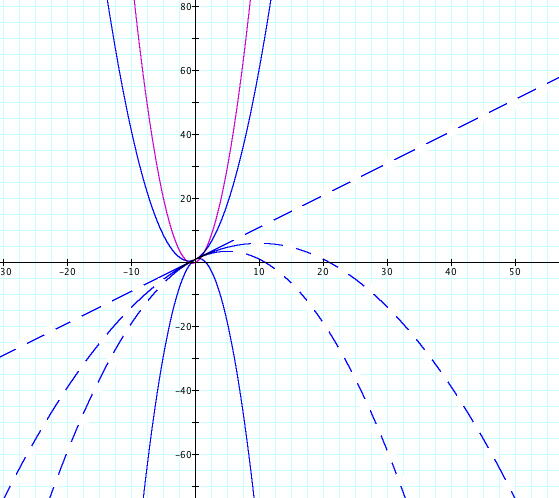
Of course, there is a segment of the quadratic equation population that never feels quite comfortable with their natural value of a and decides to permanently exist as the opposite value.
Return to Patty Wagner's home page