When Parabolas Sketch Parabolas
by Patty Wagner
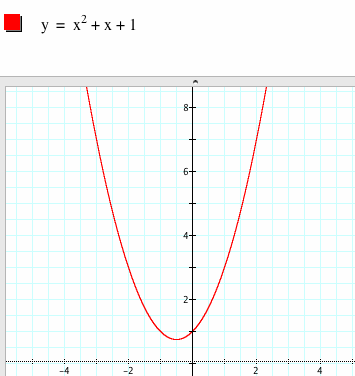
Most of us are familiar with the graph of a parabola. Here is an example as a refresher:
Something we may not all be familiar with is the interesting behavior that results when the coefficient of the middle term is changed.
This graph is y = x2 + nx + 1, where n is changing incrementally from -5 to +5. Focus carefully on the vertex of the parabola and try to ignore the rest of the graph. Notice how the point of the vertex appears to sketch an inverted parabola as it changes.
Is this actually what is happening? If so, why? And what relation does it have to our original equation?
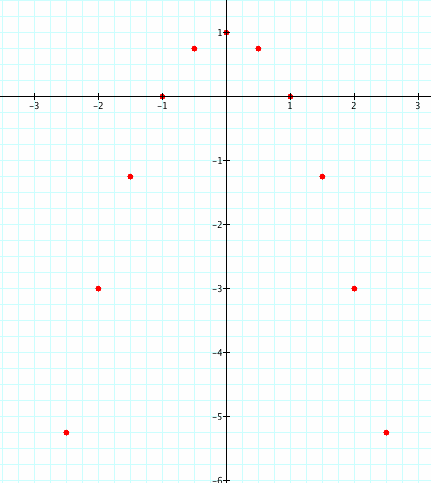
If we find the vertices of each parabola from our changing graph where n equals an integer from -5 to 5 and plot those points on a new graph we can get an accurate view of the movement of the vertices.
If we imagine a line connecting each of our points, we can see that the path does indeed form a parabola that opens downward. We also can easily see that this parabola is symmetric around the y-axis, making it very easy for us to mathematically describe it since we know parabolas that are symmetrical around the y-axis take the form y = ax2 + c. The variable c is easily identified as +1 since the parabola is shifted upwards by 1. We also know that a is negative since the parabola opens downwards. But what is the value of a? The parabola appears to be of the standard form y = -x2 + 1, but we can't take that for granted. If we insert one of our points (-2,-3), we see that our guess is correct: -3 = -22 +1
If we consider this phenomenon carefully, we realize that this second parabola (we'll call it parabola #2) creates a predictable pattern that allows us to make some assumptions. Look at the moving graph to the right.
The red parabola is a graph of the equation y = x2 + bx + 5.
The purple parabola is y = x2 + bx + 2.
The green parabola is y = x2 + bx + 1.
In each of these graphs, b is varying from -5 to 5.
Just as previously, if we look only at the vertices we can see that our parabola #2 always takes the form of y = -x2 + c, where c is the value in our equation y = x2 + bx + c. Let's explore what happens when we change the value of b in an equation of the form y = ax2 + bx + c:
We can see that not only does the opening of our parabola change when a is changed (as we would expect), but the opening of parabola #2 also changes in the same manner. This would lead us to expect that parabola #2 always takes the form y = -ax2 + c. If this is true, we would expect parabola #2 to trace an upwards path if a is negative:
Here we have y = -x2 + bx + 1 in purple and b is changing from -5 to 5. The red parabola is y = x2 + 1. It does indeed appear that the vertex of our changing parabola is following the path of an inner parabola (parabola #2).
Our original conjecture appears to be correct in that changing the coefficient of the second term in a quadratic equation produces a pattern in the form of a second parabola (parabola #2). Now we can ask why this is the case and what relation does this second parabola have to our original equation?
Recall that maximum/minimum of a function can be found by setting the derivative of the function to zero. If y = ax2 + bx +c, then y' = 2ax + b. Setting y' to zero yields 0 = 2ax + b. Therefore, the maximum/minimum of our parabola occurs when x = -b/2a. This is the x-coordinate of our vertex. If x = -b/2a, then y = a(-b/2a)2 + b(-b/2a) + c = b2/(4a) - 2b2/(4a) + 4ac/4a = [-b2/(4a)] +c.
If we analyze this general form for the vertex: (-b/2a, [-b2/(4a)] +c), we can see why we generate a second parabola when b is changed. The x-coordinate varies linearly and the y-coordinate varies quadratically as b changes. This gives us our parabolic shape. We can also easily see that the maximum (or minimum) value of y will always occur when b = 0. That explains the symmetry around the y-axis.
So, what does this second parabola have to do with our original equation? Is it useful in any way?
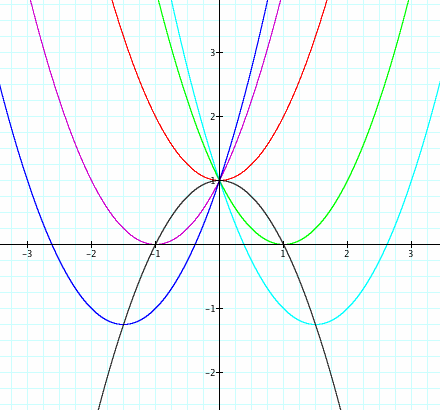
When we work with quadratic equations, we generally are interested in the "roots" - the point at which the parabola crosses the x-axis on a graph. Generally we use the quadratic equation or some other algorithm to find the point at which y = 0. Many of us have even justified the quadratic equation mathematically through proof. But let's consider the concept on a different level by using our parabola within a parabola. Consider the graph below:
This graph shows some of the parabolas that are formed when an equation of the form y = ax2 + bx + c is varied according to b. In this case, a =1, c = 1 and b is varying from -3 to 3. Each value of b is represented by a different color parabola and our parabola #2 is noted in black.
Notice that some of these parabolas cross the x-axis, some just touch the x-axis, and some do not cross the x-axis at all. We will find real roots for each of the equations except the one represented by the red parabola. If we examine our parabola #2 which is depicted by the black parabola, we can predict graphically which parabolas will have real roots depending on the value of b. As b gets closer to zero from either side, the graph is raised above the x-axis and we have no roots. As the absolute value of b becomes greater, the vertex will slide down our parabola #2, guaranteeing that we will continue to have real roots.
So let's put this all together but identifying the different situations that we can have:
a positive and c positive
a positive and c negative:
a negative and c negative
a negative and c positive:
All these moving graphs can get confusing, but if we look at them one at a time, we see that when a and c are of opposite sign (positive or negative), we will always have real roots no matter what the value of b. (We can also see this will be the case if c = 0.) However, when a and c are the same signs, whether the roots of the equation are real depends on the value of b.
Let's focus on these two cases (represented in the red graphs above). We've seen that when y = ax2 + bx + c, changing the value of b creates a parabola inverted to y = ax2 + bx + c. Its maximum/minimum occurs when b = 0. This suggests that regardless of the value of a and c, we can find b that, if its absolute value is sufficiently large, will result in an equation with real roots. Where does this occur?
If we trace parabola #2, we will obtain real roots when the vertex of parabola #2 falls on the x-axis and every point further away from the vertex of parabola #2. So the absolute value of b must be, at a minimum, the value obtained when the vertex of y = ax2 + bx + c falls on the roots of y = -ax2 + c (the equation of parabola #2). This would be when x2 = c/a, so x equals +/- the square root of c/a. To obtain a vertex with x-coordinate x = +/-&radic(c/a) from the graph y = ax2 + bx + c,
-b/2a must equal +/-&radic(c/a). Solving for b,
-b/2a = &radic(c/a)
b2/4a2 = c/a
b2 = 4ac
So to have real roots, b2 must be greater than or equal to 4ac. You may recall that b2 - 4ac is called the "discriminant" of a quadratic equation. We now can understand graphically why the discriminant reveals the nature of the roots of the equation. We also can see that our "parabola within a parabola" is not so mysterious after all!
Return to Patty Wagner's home page