Written by Sunny Yoon
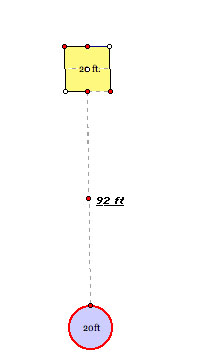
Farmer Jones had a goat on a tether. He tied the end of the tether not attached to the goat to a stake in a field. Over what area could the goat graze? Of course you need to know something about the length of the tether and about the field. There are two structures in the field: -- a shed that is 20 ft long and 20 feet wide (square) -- a silo that is 20 ft in diameter The center of the shed and the center of the silo are on a line and the distance apart is 92 feet. The distance from center to center, if you wanted to use this data, is 112 feet. The tether for the goat is 76.7 feet long. The stake to which the tether is tied is somewhere along the line of centers between the shed and the silo. Explore the area over which the goat can graze as the stake is moved along this line segment from the midpoint of the side of the shed to the edge of the silo.
Here is the picture I'm working with.
Imagine if there was no barn or the silo here. I'm going to draw a diagram where it be show the maximum area when there is no barn or silo in the picture.
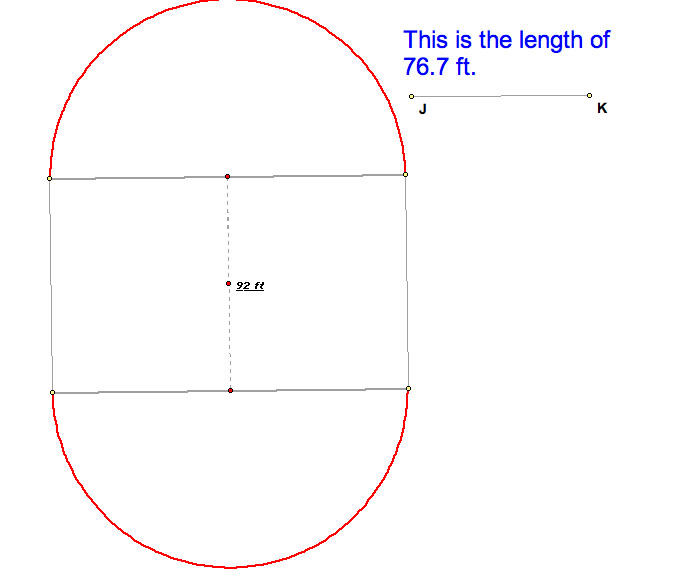
Without the barn or silo, it's easy to calculate the area here.
So the total area here is 32594.44 feet square.
I took 76.7 feet and rotated it 90 degrees along the bottom edges of the barn. Then there should two vertical straight segments (76.7ft - 20ft) at the top of the edges of the barn. Then with the center at the bottom edge with the new radius (76.7ft - 10ft), I constructed two circles. I found the intersections of those two circles. That would be the maximum grazing area of the goat if the goat is tied down to the center of the barn.
Here's the picture I got for the maximum grazing area of the barn. The red arcs represents the original maximum grazing area without the barn.
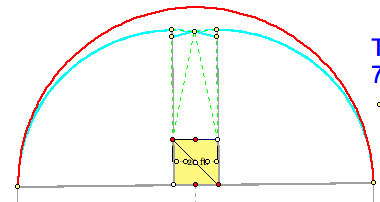
First of all, let's subtract the area of the barn from the original semicircle. This is to make sure that the overall maximum grazing area should be less than this number.
9216.74 - 400 = 8816.74 feet square
The overall maximum grazing area I'll get should be less then 8816.74 feet square.
The easiest way to find the grazing area is to divide the sections up. Here's the picture how I divided the area into five different sections.
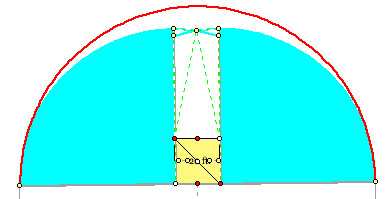
First, I found the areas of the two sectors.
The radius of one sector is 76.7 - 10 = 66.7ft and it's one-fourth of a circle.
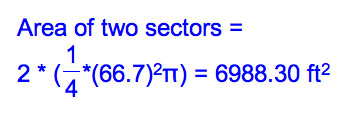
Now, we need to find the area of a triangle and two sectors surrounding the triangle.
First of all, the triangle inside will be an isosceles triangle. Therefore, the altitude is going to be a perpendicular bisector. Let's find the hypothesis of the isosceles triangle.
From the midpoint of the barn to the end of the sector is 76.7ft. So, when you rotate the rope 90 degrees, it will be a vertical line which is measured at 66.7ft. Using the shortened rope, you are going to go around the edge of the barn, so you need to take 20ft away. Therefore the hypothesis of the isosceles triangle will be 46.7ft.
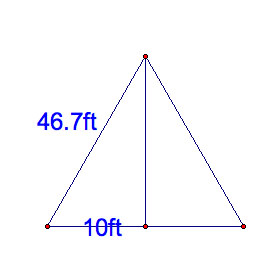
Using the Pythagorean Theorem, I'll find the altitude to be 45.62 ft.
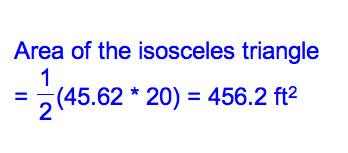
Now it's time to find the area of the two sectors surrounding the isosceles triangle. In order to find an area of a sector, we need to know the angle. If you look at the angle created by sector + triangle at the top edge of the barn, it equals to 90 degrees. Then, we can find the base angle of the isosceles triangle using inverse cosine.
Now, since you know the radius of the sector and the angle, let's find the area.
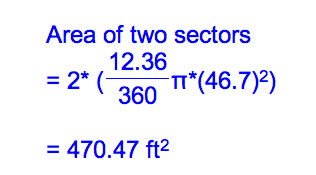
Therefore, the maximum grazing area around the barn = (Area of two big sectors) + (Area of an isosceles triangle) + (Area of two smaller sectors). That equals to 6988.30 + 456.2 + 470.47 = 7914.97 feet square.
8816.74 feet square = Maximum Area without the barn > 7914.97 feet square = Maximum Area with the barn
Now, it's time to find the area around the silo. Like the previous example using the barn, let me find the maximum area by subtracting the area of the silo from the area of the original semicircle. That is to ensure that our maximum grazing area around the silo will be less than this number.
9216.74 - (314.16) = 8902.58 feet square
The overall maximum grazing area I'll get should be less then 8902.58 feet square.
Finding the grazing area around the silo was a lot harder than it looked. Imagine if the rope went around the circle. The length of the tether is 76.7 ft. As the tether goes around the silo, the grazing area will decrease. If the tether goes around the silo in the other direction, there will be an overlapping area.
I'm going to look at half of the picture in order to have a better mathematical approach.
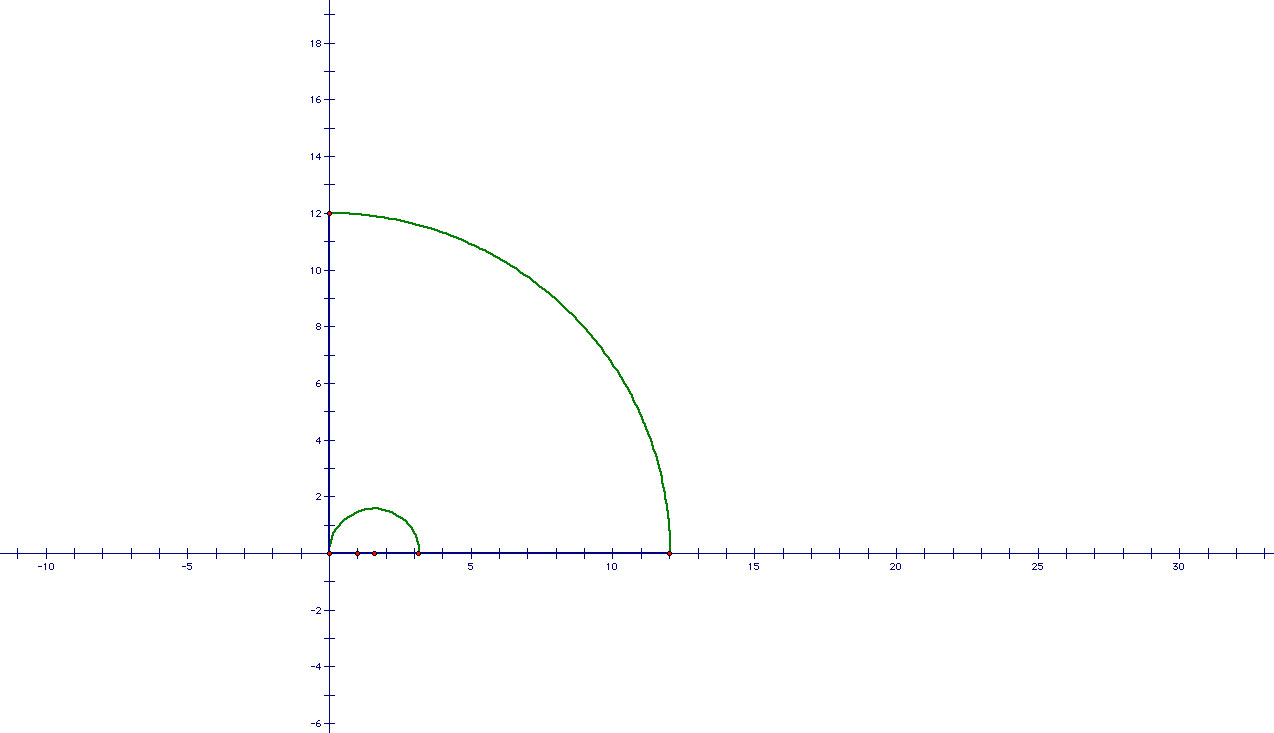
The outside arc represents the arc created by the tether 76.7 ft. The smaller semicircle is half of the silo.
Now, I'm going to imagine if the tether goes all the around half of the silo.
When you add 45.3 ft to 20 ft (the diameter of the silo), you end up with 65.3 ft which is approximately 11.4 ft shorter from the original length of the tether.
I'm going to use 65.3 ft as the radius to find the sector area (with the area of semi silo inside).
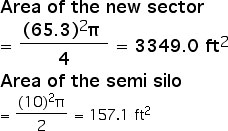
So the area of half of the maximum grazing area is 3349 - 157.1 = 3191.9 feet square.
Therefore the total area of the maximum grazing area around the silo is 6383.8 feet square.
TOTAL GRAZING AREA = 14112.8 + 7914.97+ 6383.8 = 28411.57 feet square