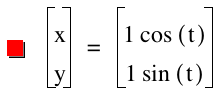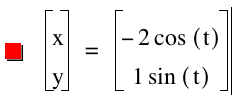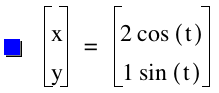Assignment 10 :: Parametric Equations
By Jamie K. York
![]()
Let's explore the parametric equations below for 0 ² t ³ 2¹.
x = a cos(t)
y = b sin(t)
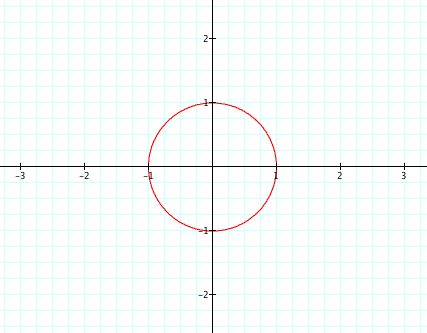
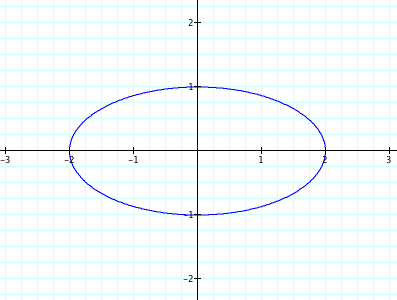
As we saw with the quadratic equations, modifications of the variables resulting in various patterns in the resulting graphs. We will start with a value of 1 for both a and b. See the resulting graph below.
|
|
|
Note that this configuration results in a circle. To explore additional configurations where a = b, review the animated graph below.
What happens when these variables are not equal? Let's investigate further to see.
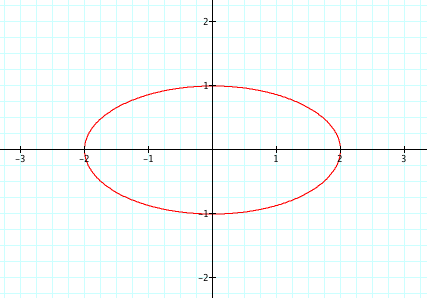
For each graph, one variable has been set constant at a value of 1. As the additional variable changes between 2 and 4, we notice that these modifications form the shape called an ellipse. This differs from the circle resulting from a = b. However, with either confirguration, it is clear that the values of a and b stretch or shrink the figure.
Note that for a t range of 0 ² t ³ 2¹, the values of +a and -a result in the same graph. The same applies to the b variable.
|
|
|
|
|
|
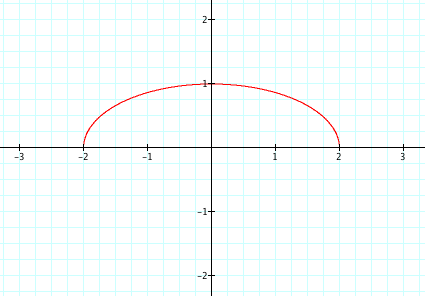
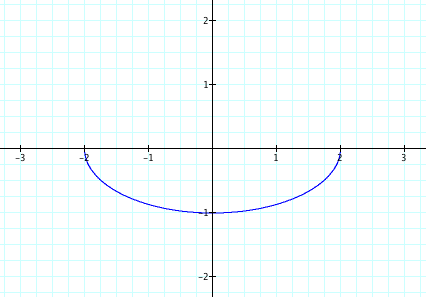
Does the result change with a modification to the range of t? Explore the same graphs below with various t values to find out.
|
|
|
|
|
|
Home | EMAT 6680 |
Dr. Jim Wilson