
Assignment
11 :: Polar Equations
Exploring r
= a + b cos (kθ)
By Jamie K.
York

The
polar coordinate system is a two-dimensional system that identifies a point by
a distance and an angle. The distance is measured from a fixed point, 0, and
the angle is measured from a fixed direction, 0 degrees.

A
basic trigonometric equation that can be graphed on a polar coordinate plane is
the cosine function. This particular graph is referred to a limaćon, sometimes
called the limaćon of Pascal. As the given variables are modified, various
graphical displays can be explored. We can see three variations, including
dimpled limaćons, limaćons with cusp (cardiod), and looped limaćons.
r = a + b cos (kθ)
First,
let us look at the version where variables a, b, and k are set to zero, or r = 1 + 1 cos (1θ).
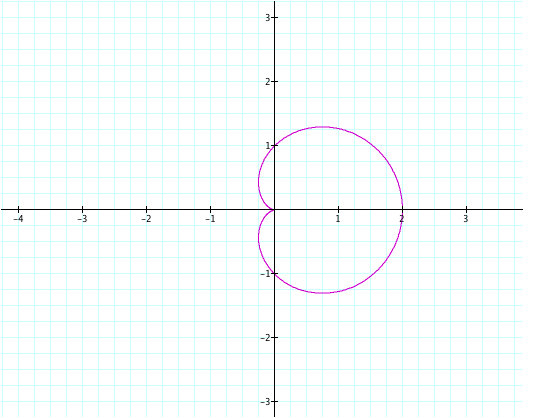
Variable
a
If
this is our origin, we can make modifications to each variable to see how it
impacts the graphical display. First, let us try modifications to variable a. The
animation below displays a as it changes from -3 to 3. Notice that the graphical display at
-3 is the same as that at 3. The same occurs for -2 and 2, as well as -1 and 1.
As we modify variable a, it alters the y-intercept of the graph. For an a value of
-1 or 1, the y-intercept is -1 and 1. For an a value of -2 or 2, the y-intercept is
-2 and 2. This expands the figure both horizontally and vertically.
Another
way to view this is by graphing multiple modifications simultaneously, allowing
you to compare and contrast each modification to another. This visualization
also makes it more clear how an a value of -a or a results in the same
graphical display.


Variable
b
Next,
changing a
back to 1, let us make modifications to variable b. The animation below displays b as it changes
from -3 to 3. Note that the b value is that which is centered between the large
loop’s x-intercept and the small loop’s x-intercept. Another observation that
can be made is the reflexive property that exists between the graph when b is -b and
b. For the b
value of -1 and 1, the smaller loop disappears, creating a heart shape. This
continues as the b value moves closer to zero, where the graph then reflects a
circle of radius 1.
Below
is a graph of each integer value of b in the same range, [-3, 3]. This visual
makes the reflexivity of some of the graphs more evident.


Variable
k
Finally,
by changing b
back to 1, we can explore modifications to variable k. The animation below displays k as it
varies from -3 to 3. As with the a variable, corresponding positive and
negative values of k reflect the same graphical representation. The value of 0
represents a circle of radius 1. As the value of k increases, or decreases, the shape
begins to change more drastically. This unique shape turns into a flower-like
shape as the value of k increases. The number of petals is determined by the value of k.
If k is odd, then k petals are generated. If k is even, then 2k petals are
generated.


What happens when a = b?
To extend this exploration, we can examine the attributes
of the graph when a = b (see examples below). In this exploration, we can see that graph
with -a and -b creates the reflection of the graph with a and b over the
y-axis. Setting these variables equal maintains the original heart shape that
we viewed. As the variables
increase, this shape grows both horizontally and vertically.


What
happens when a = 0?
Another
variation to explore is when a = 0 and the remaining equation is r = b cos (kθ). The shape here
remains a circle. As the variable b is increased, the diameter of the circle
increases. However, regardless of the variable, the circle remains anchored at
the origin, (0, 0).


Summary
In summary, we can make the
following conclusions about these graph of r = a + b cos (kθ):
When k = 1, we have a figure
called a limaćon.
If b = 2a, then the
limaćon is a trisectrix.
If b < a, then
the limaćon has an inner loop.
If a = b, then the
limaćon is a cardiod.
If 2a > b > a,
then the limaćon is dimpled.
If b ≥ 2a, then the
limaćon is convex.
When k = 1 and a = 0, a
circle is generated along the x-axis with a diameter of |a|.
When a = 0, a rose figure is
generated.
The figured will
have on petal on the positive x-axis, with a radius of |a| for each petal.
If k is odd, then k
is the number of petals.
If k is even, then
2k is the number of petals.
What about sine?
When we change our original
function to sine, we have r = a + b sin kθ.

With this graph, we first
notice that the figure is now oriented on the y-axis as opposed to the x-axis.
Many of the other characteristics remain the same, although maintaining the new
orientation.
Home | EMAT 6680 | Dr. Jim Wilson