
Assignment 4 :: Concurrencies of a Triangle
The Nine
Point Circle
By Jamie K.
York
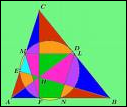
The nine-point circle is a unique relation
between the altitudes of the triangle, the midpoints of its sides, and the
midpoints between the orthocenter and each vertex.
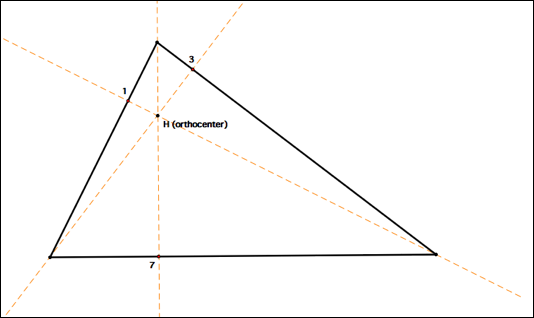
Begin by finding the
altitudes of the given triangle, marking the intersection of each altitude with
the side of the triangle. Note that these three lines intersect inside the
triangle at a single point called the orthocenter.
Now, find the midpoints on
each side of the triangle.
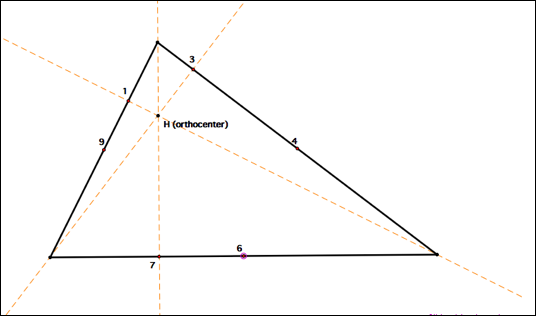
Also find the midpoints
between the orthocenter and each vertex.
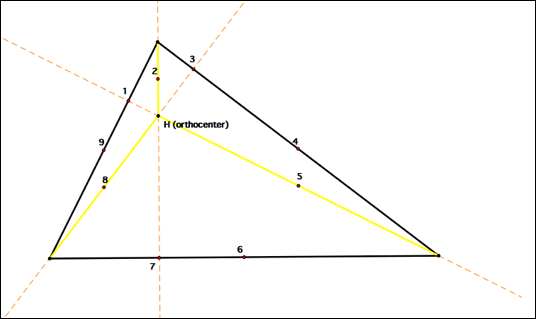
These nine points are those
that will align on the circumference of the constructed circle. In order to construct
the circle properly, we will first find the center. To find the center, create
an inscribed triangle by connecting the midpoints of the sides of the original
triangle. Find the center of the inscribed triangle by connecting the
perpendicular bisectors. The center of the inscribed triangle is also the
center of the nine-point circle. We can now more accurately construct the
circle.


Further Exploration
The triangle used above is
acute. Can the nine-point circle be constructed the same way with a right or
obtuse triangle?
Check out this animation to
see more: GSP
Nine-Point Circle Animation
Home | EMAT 6680 | Dr. Jim Wilson