Assignment 6 :: Medians
By Jamie K. York
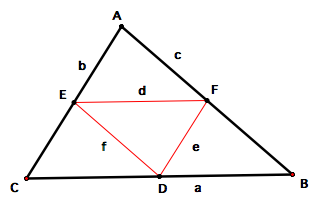
The medians of a triangle are the midpoints of each of the three segments, or sides. A triangle of medians is constructed by constructing the segments formed by these three points. Any example is shown below. This particular example is an acute triangle. Let's explore four types of triangles (acute, equilateral, isosceles, and right) and their resulting triangle of medians.
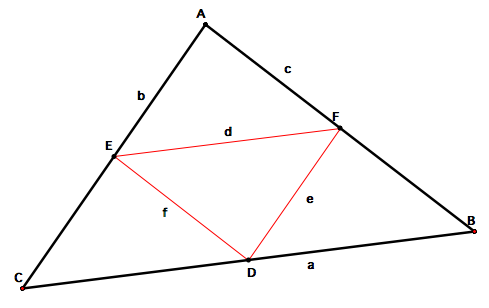
Acute Triangle
Recall that an acute triangle has three angles each measuring less than 90 degrees. The triangle below is an example. The measurements of the original triangle and resulting triangle of medians show that angle measures remain unchanged. Thus, the triangle of medians of an acute triangle is an acute triangle as well.
|
|
|
|
Further analysis of the segments shows that the triangle of medians has segment lengths half the size of the original triangle.

To further explore acute triangles, use the GSP file here.
Equilateral Triangle
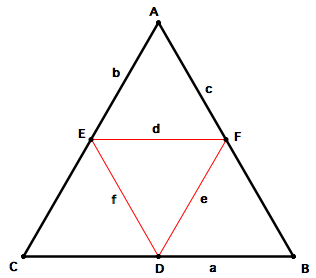
Recall that an equilateral triangle has three sides of equal measure and three angles measuring 60 degrees each. The triangle below is an example. The characteristics of the equilateral triangle and its triangle of medians are the same as those of the equilateral triangle. Since the equilateral triangle is a specific type of acute triangle, this pattern seems to make since. So, we see that these hold for this specific example. The measurements of the original triangle and resulting triangle of medians show that angle measures remain unchanged. Thus, the triangle of medians of an equilateral triangle is an equilateral triangle as well.
|
|
|
|
Further analysis of the segments shows that the triangle of medians has segment lengths half the size of the original triangle, again, showing that this specific example of an acute triangle maintains this ratio of segment measures.

To further explore equilateral triangles, use the GSP file here.
Isosceles Triangle
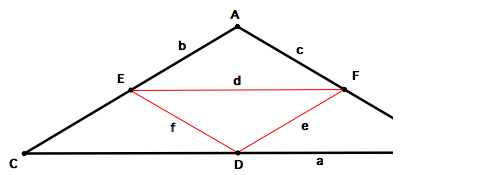
Recall that an isosceles triangle has two sides of equal lenght and two angles of equal measure. The triangle below is an example.Once again, the measurements of the original triangle and resulting triangle of medians shows that angle measures remain unchanged. Thus, the triangle of medians of an isosceles triangle is an isosceles triangle as well.
|
|
|
|
Further analysis of the segments shows that the triangle of medians has segment lengths half the size of the original triangle. Another characteristic that we saw in both acute and equilateral triangles. We see that constructing the segments between the medians in fact creates four similar isosceles triangles.

To further explore isosceles triangles, use the GSP file here.
Right Triangle
Recall that an acute triangle has one angle measuring exactly 90 degrees. Here is an example. With this triangle, we see the same characteristics as we did with the previous three types of triangles. We also see the same creation of four similar triangles as we did in the isosceles triangle.
|
|
|
|

To further explore right triangles, use the GSP file here.
Home | EMAT 6680 |
Dr. Jim Wilson