Assignment 7 :: Tangent Circles
By Jamie K. York

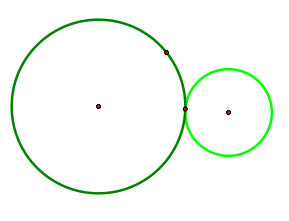
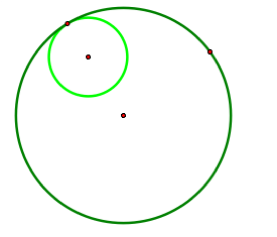
Two circles are tangent when the intersect at one and only one point. Below are two examples of circles that are tangent to one another. The first example is where one circle lies inside of the other, and the other example is where neither circle is within the other.
|
|
|
Let's look further to explore the construction of a circle tanget to two given circles.
Example 1 (GSP file)
Example 2 (GSP file)
Each example contains a script tool that allows you to recreate a circle tangent to two given circles. Use this to further explore the various examples and characteristics of tangent circles.
Another interesting aspect of tangent circles is exploring the figures and designs created by the tracing of certain points. Use the example below to further explore this idea in.
Tracing 1 (GSP file)
Notice that Tracing 1 highlights the center of the circle tangent to the two given circles. As it rotates, we see that the tracing of its center constructs an elipse with foci at the centers of the two given circles. Take a look at few different sets of two given circles, their tangent circle, and the tracing of the center of that circle. A few examples to try are a circle within a circle, a circle tangent to a circle, and two circles outside of one another.
Tracing 2 (GSP file)
Tracing 2 highlights a random point on the circle tangent to the two given circles. As this point is traced, we see that it constructs an elipse that is tangent to the two given circles as well. Change the orientation and size of the two given circles to see how the tracing is impacted.
Tracing 3 (GSP file)
Tracing 3 highlights two random points on the cirlce, showing that the same observation from Tracing 2 occurs. Again, change the orientation and size of the two given circles to see how the tracing is impacted.
Home | EMAT 6680 |
Dr. Jim Wilson