
Assignment 9
:: Pedal Triangles
By Jamie K.York
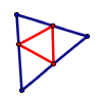
A pedal triangle for a specified point P and triangle ABC can be found using the perpendiculars from each side of the triangle to this point. The intersection points of the triangle sides (extended if necessary) and the perpendilar lines form the pedal triangle. Use the GSP file to further explore pedal triangles for a variety of points and triangle types. Notice that pedal points within the triangle form pedal triangles within the triangle.
To create additional pedal triangles, use the pedal triangle script tool (GSP file).
It seems as though pedal triangles could continue indefinitely. If we begin to explore pedal triangles within pedal triangles, we begin to see some similaries. Review the figures and measurements below to see what relationships exist between the triangles.
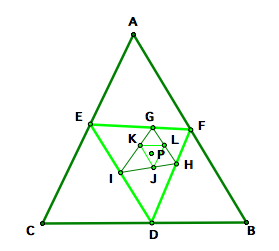

Notice that the third pedal triangle, JKL, has the same angle measurements as the original triangle, ABC. The third pedal triangle is thus similar to the original triangle. Explore variations of the original triangle and pedal point using the GSP file.
Further Exploration
* Does the patten continue with infinitely more pedal triangles?
* Does the pattern remain the same regardless of the pedal point location?
Home |
EMAT 6680 |
Dr. Jim Wilson