
Final Project :: One Final Exploration
The Cycloid
By Jamie K. York
![]()
The cycloid is the locus of a point on the
rim of a circle of radius a rolling along a straight
line. It was investigated and name by Galileo, with many additional researchers
to follow. Gear teeth were initally constructed using the cycloid configuration.
Graphing
Calculator
In
parametric form, as discussed in assignment 10, the cycloid can be graphed as
shown below:
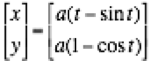
![]()
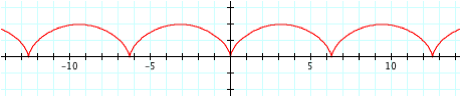
The
cycloid can also be written in a Cartesian form:
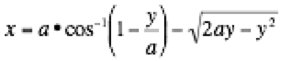
Geometer's
Sketchpad
To
construct a cycloid, following these instructions:
1. Define a Cartesian coordinate system.
2. Create a circle of a given radius,
preferrably in the upper right corner of the window.
3. Label the center of this circle O. Create
a movable point on the circle and label it A.
4. Graph the function f(x)=1.
This is the equation of the horizontal line y=1.
5. Create a movable point O' on this line.
6.
Highlight the center of circle O and the movable point O'. Then choose from the
menu bar
transform
> mark vector. This is where we want to translate the
circle on the right upper corner.
7.
Now highlight the center O, the movable point A, and the circle. Then choose
from the menu bar transform > translate (use the defaults
and click translate). In this way we get a copy of the circle on the y=1 line.
8. Select the point O' and the point A'. Edit
one animation button for these points. Note: We want to animate the center of
mass point O' forward and the point A clockwise.
9. Mark sure that you enable the trace option
for point A. This point will generate the cycloid.
The
construction should resemble this GSP file.
Home | EMAT 6680 |
Dr. Jim Wilson