Parametric Equation

P a r a m e t r i c E q u a t i o n

Jane Yun

Let x = f (t) and y = g (t), where f and g are two functions whose common domain is some interval I. The collection of points defined by

(x, y) = (f (t), g (t))

is called a plane curve. The equations

x = f (t) y = g (t)

where t is in I, are called parametric equations of the curve. The variable t is called a parameter.

Parametric equations are particularly useful in describing movement along a curve. Suppose that a curve is defined by the parametric equations

x = f (t), y = g (t), a ≤ t ≤ b

where f and g are each defined over the interval a ≤ t ≤ b. For a given value of t, we can find the value of x = f (t) and y = g (t), obtaining point (x, y) on the curve. In fact, as t varies over the interval from t = a to t = b, successive values of t give rise to a directed movement along the curve; that is, the curve is traced out in a certain direction by the corresponding succession of points (x, y).

Now, let’s investigate parametric equation

x = a cos (t)

y = b sin (t)

by varying a and b.

Let’s begin exploration when a = b.

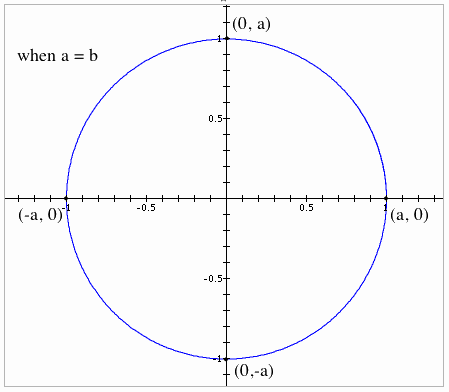
Notice that the curve is a circle with center at (0, 0) and radius a. As the parameter t increases, say from t = 0[the point (a, 0)] to t = Π/2 [the point (0, a)] to t = Π [the point (-a, 0) to t = 3Π/2 [the point (-a, 0)], we see that the corresponding points are traces in a counterclockwise direction around the circle. Since a = b, as 'a', which is the radius, changes, it just changes the radius of a circle.

The presence of sines and cosines in the parametric equations suggests that we use a Pythagorean identity. In fact, since

cos t = x/a sin t = y/a

we find that

cos² t + sin² t = 1

(x/a)² + (y/a)² = 1

x² + y² = a²

Let’s discuss the curve further. The domain of each parametric equations is -∞ < t < ∞. Thus, the graph is actually being repeated each time that t increases by 2п.

If we wanted the curve to consist of exactly 1 revolution in the counter clockwise direction, we could write

x = a cos t, y = a sin t, 0 ≤ t ≤ 2п

This curve stats at t = 0 [the point (a, 0)] and, proceeding counterclockwise around the circle, ends at t = 2п [also the point (a, 0)].

Next, let’s try when a > b.

Let a = 2 and b = 1.

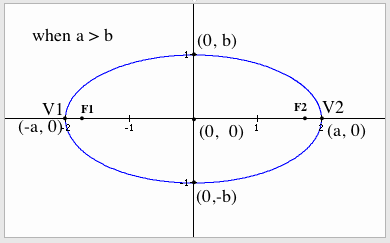
Notice that the graph above is an ellipse. An ellipse is the collection of all points inthe palne the sum of whose distances from two fixed points, called the foci, is a constant.

The curve is an ellipse with center (0, 0) and foci at (-c,0) and (c, 0). The foci are labeled F₁ and F₂. The line containing the foci is called the major axis. The midpoint of the line segment joining the foci is the center of the ellipse. The line through the center and perpendicular to the major axis is the minor axis.

The two points of intersection of the ellipse and the major axis are the vertices, V₁ and V₂, of the ellipse. The distance from one vertex to the other is the length of the major axis. The ellipse is symmetric with respect to its major axis, with respect to the minor axis, and with respect to the center.

Again, since The presence of sines and cosines in the parametric equations suggests that we use a Pythagorean identity. In fact, since

cos t = x/a sin t = y/b

we find that

cos² t + sin² t = 1

(x/a)² + (y/b)² = 1

where a > b > 0 and b² = a² – c². This is the ellipse equation with center at (0, 0) and foci at (-c, 0) and (+c, 0).

As you can verify, the ellipse defined by equation above is symmetric with respect to the x-axis, y-axis, and origin.

Because the major axis is in the x-axis, we find the vertices of the ellipse defined by equation above by letting y = 0. The vertices satisfy the equation (x/a)² = 1, the solution of which are x = +a and –a. The y-intercepts of the ellipse, founded by letting x = 0, have coordinates (0, -b) and (0, b). These four intercepts, (a, 0), (-a, 0), (0, b), and (0, -b) are uses to graph the ellipse.

For further investigation, let’s try when a < b.

I’m going to let a = 1 & b = 2.

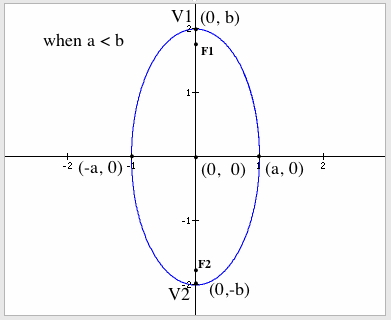
This is figure illustrates the graph of such an ellipse. Notice the right triangle with the points at (0, 0), (b, 0), and (0, c). Now, let’s find the equation of an ellipse when the major axis is in the y-axis in terms of x and y.

Since

cos t = x/b sin t = y/a

we find that

cos² t + sin² t = 1

(x/b)² + (y/a)² = 1

where a > b > 0 and b² = a² – c². An equation of this ellipse is center at (0, 0) and foci at (0, -c) and (0, +c). The major axis is the y-axis; the vertices are at (0, -a) and (0, a).

Look closely at equations when a > b and when a < b. Although they may look alike, there is a difference. In equation when a > b, the larger number, a², is in the denominator of the x²-term, so the major axis of the ellipse is along the x-axis. In equation when a < b, the larger number, a², is the in the denominator of the y²-term, so the major axis is along the y-axis.

Returen to Jane's Homepage