P
o l a r E q u a t i o n
by
Jane Yun
The
locus of a point in the plane that moves so that its distance from a fixed
point (focus) is in constant ratio to its distance from a fixed line
(directrix) is a conic. The constant
ratio is the eccentricity of the conic and is denoted by e.
Moreover, the conic is an ellipse if e
< 1, a parabola if e = 1,
and a hyperbola if e > 1.
We will look into the polar equations of
conics of the following:
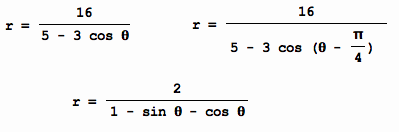
LetŐs look at
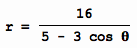
This is a polar equation of conic with focus
at the pole and directrix perpendicular to the polar axis at a distance to the
left of the pole, which is
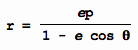
where e is the eccentricity of conic.
The given equation is not quite in the form
of above equation since the first tem in the denominator is 5 instead of
1. We divide the numerator and
denominator by 5 to obtain
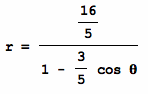
Then,
We conclude that the conic is an ellipse
since e Ü 1. To check and see if
our conclusion is correct, letŐs look at the graph.
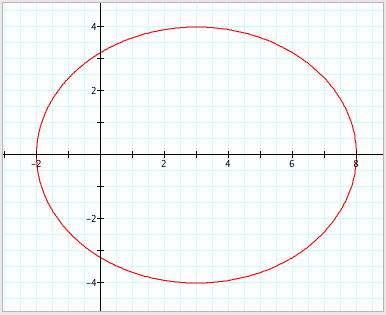
From the observation of a graph, we can see
that there is symmetry. LetŐs test
for symmetry.
Polar Axis: Replace q
by – q. The
result is
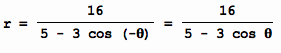
The test is satisfied, so the graph is
symmetric with respect to the polar axis (x
– axis)
The Line θ = P/2:
Replace q
by (P
– q). The result is
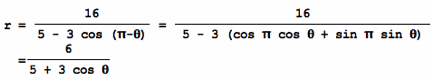
The test fails, so the graph may or may not
be symmetric with respect to the line q = P/2 (y
– axis).
The Pole: Replace r by –r.
Then the result is
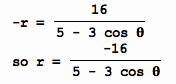
The
test fails, so the graph may or may not be symmetric with respect to the pole
(origin).
Therefore, the conic is ellipse, and the
graph is symmetric with respect to the polar axis.
Next, letŐs look at
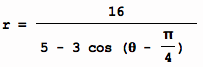
By using the same process above, we can
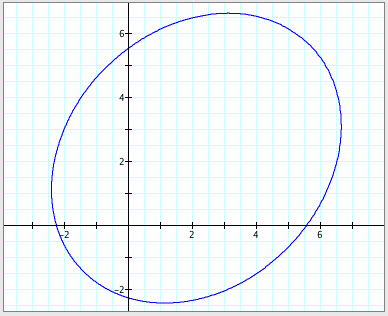
conclude that the conic is an ellipse since e = 3/5 and e < 1. Because q is replaced by q –
(q/4),
the x-axis and y-axis are rotated through an angle q/4 while
the origin remains fixed. Look at
the graph below and see if our conclusion is correct.
Now, letŐs investigate following equation
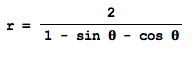
The equation is not a polar equation of
conics because it is not one of the forms below.
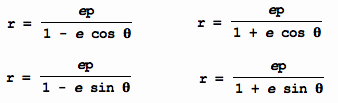
But the equation is in the form of a polar
equation. LetŐs look at the graph for further investigation.
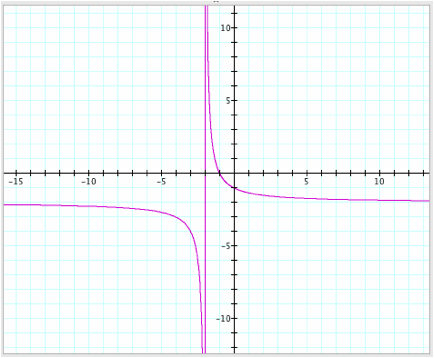
By looking at the graph, x = -2 is a vertical asymptote. This means that
- as x approaches -2+, the values R(x) approach °
- as x approaches -2-, the values R(x) approach -° .
The graph of a function will never
intersect a vertical asymptote.