T r e e D a t a
by
Jane Yun
In this exploration, the focus will be on the use of
spreadsheets to investigate mathematical relationships. With the given data, the spreadsheet
enables us to see the relationship between two variables like explanatory (x)
and response (y) variables.
We will use EXCEL to solve the problem to predict the number of
board feet of lumber per tree that is missing from the given data, but first we
will find the function that fits with the given data.
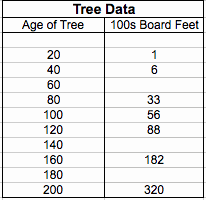
The tree data is from the lumber industry, which gives the approximated
number (#) of board feet of lumber per tree in the forest of a given age.
LetŐs plot the given data and observe the graph.
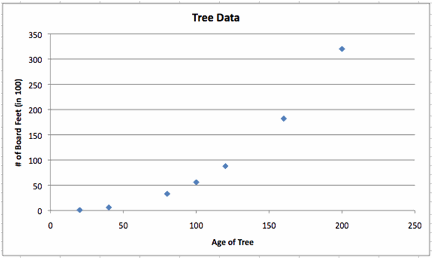
By looking at the graph, it looks like the function might be
quadratic. It cannot be the exponential function, f(x) = ax, where
a is the base and is positive. Also, a
1 because, in the exponential function, the y-intercept is at (0, 1); hence,
the given data cannot be the exponential function.
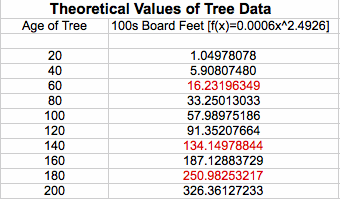
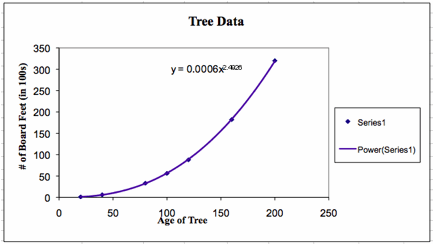
The predicted function from the EXCEL is f(x)
= 0.0006x2.4878.
Thus, the function is not a quadratic; it is a power function. The power function is a function whose
value is the product of a constant and a power of independent variable.
LetŐs calculate the measure of error of each data point and the
average value of square measured errors to see how close to the actual data.
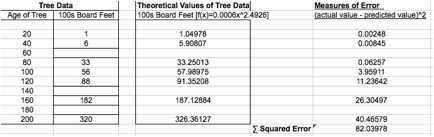
Then, we can calculate the average of squared errors, which is
the sum of squared errors divided by the number of data points, is 5.1967, and
by square rooting the average of the squared errors, the standard error can be
found, which is 2.2796. Since the standard error of 2.2796 is pretty small,
f(x) = 0.0006x2.4878 fit the
data.
By using the function above, the predicted harvest for age of
tree, 60, 140, & 180 are 16.23, 134.15, & 250.98.