
Q U A D R A T I C E Q U A T I O N
by
Jane Yun
With many available technologies, it has become
possible to construct graphs following equation.
ax2 + bx + c = 0
Also, it can overlay several graphs of
y = ax2
+ bx + c
for different values of a, b, or c as the other
two are held constant. From these
graphs, we can discuss the patterns for the roots of
ax2 + bx + c = 0
Investigation
1. Changing ŌbÕ
LetÕs start the investigation when b = -3, -2,
-1, 0, 1, 2, 3 for the following quadratic equation.
y = x2 + bx
+ 1
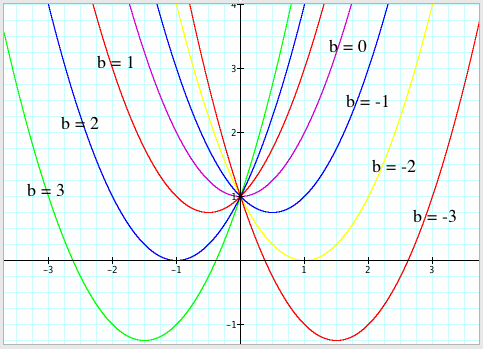
From observing the graph above, the shape of
graph is a parabola. The parabola
shifts to right or left as b changes
and always passes through the same point on the y-axis at (0,1). For b < -2, the parabola passes
through the x-axis twice with positive x values; that is, the equation has two
positive real roots. For b > 2,
the parabola passes through the x-axis twice with negative x values. This indicates that the equation has
two negative real roots. For b = -2, the parabola is tangent to the
x–axis, so the original equation has one real positive root at the point
of tangency. Again, for b = 2, the
parabola is tangent to the x-axis.
Thus, the original equation has one real negative root at the point of
tangency. For -2 < b < 2, the parabola does not pass
through the x-axis. This means
that the equation has no real roots.
Investigation
2. The xb- plane
LetÕs consider the following equation.
x2 + bx
+ 1 = 0
By setting b
= y, you get the following graph.
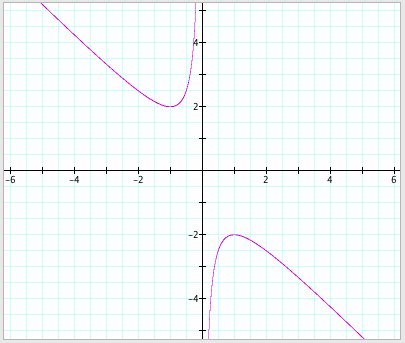
Notice that there is a vertical asymptote at x =
0. When b = 2, the graph is
tangent to y = 2, so this equation has one real negative root at the point of
tangency. Again, when b = -2, the graph
is tangent to y = -2. Thus, this
equation has one real positive root at the point of tangency.
Now, if we take any particular value of b, such as b = 5, and overlay this equation on the graph, we add a line that
is parallel to the x-axis. If b = 5
passes through the curve in the xb plane, the intersection points aligns to the
roots of the original equation for that value of b. Look at the graph
below.
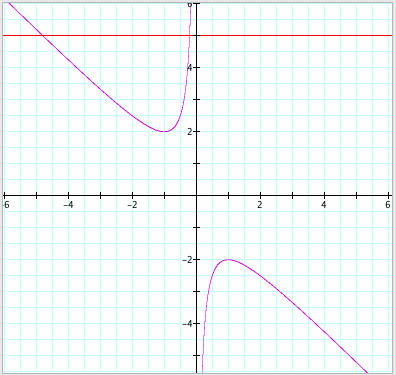
For each value of b, we get a horizontal
line. By looking at the graph
above, it clearly shows that we get two negative roots of the original equation
when b > 2, one negative real root when b = 2, one positive real root when b
= -2, no real roots for -2 < b < 2, and two positive real roots when b
< -2.
Investigation
3. When c = -1
LetÕs consider following equation.
x2 + bx
- 1 = 0
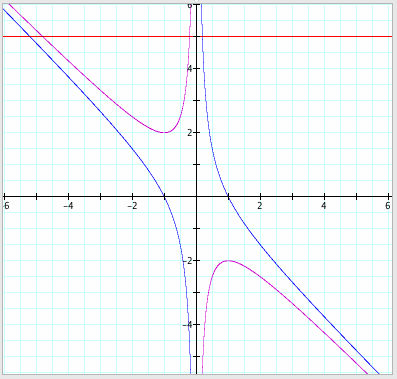
Notice that there is still a vertical asymptote
at x = 0 and the shape of graph is a hyperbola.
If
we take any particular value of b,
such as b = 5 again, and overlay this equation on the graph,
we add a line that is parallel to the x-axis. If b = 5 passes through the curve in the xb plane, the intersection
points aligns to the roots of the original equation for that value of b.
It is clear that, for
each value of b, we will get a
horizontal line and intersects the graph of original equation, x2 + bx
- 1 = 0, at two points.
This indicates that the original equation has two real roots for every
value of b.
LetÕs explore more by varying the values of c.
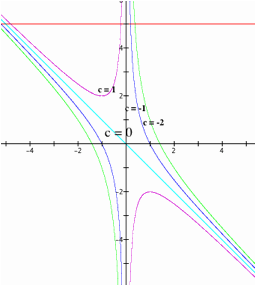
By looking at the graph
above, the equation, x2 + bx + c = 0, always has one real root when
c = 0. For c > 0, the equation
can have among two real roots, one root, or no root. When c < 0, the equation always have two real roots –
one positive and one negative.