Nine-Point Circle

By

Jane Yun

 

 

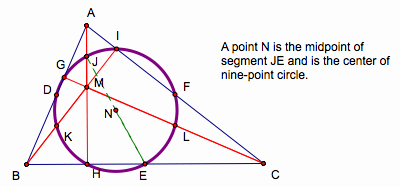
The nine-point circle is a circle that can be constructed for any given triangle.  It is so named because it passes through nine significant points, six lying on the triangle itself. They include: the midpoint of each side of the triangle, the foot of each altitude, and the midpoint of segment of each altitude from its vertex to the orthocenter, where three altitudes meet.

 

 

 

We will construct the nine points, locate the center, N, and construct the nine points.

 

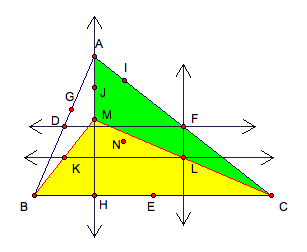
First, draw any triangle.

 

 

Find the midpoints of the sides of ÆABC, which are points D, E, & F.

 

 

 

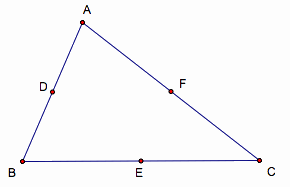
Next, draw a perpendicular line from each vertex to the line of the opposite side, which is an altitude.  Point M is the orthocenter of ÆABC.

 

 

 

 

 

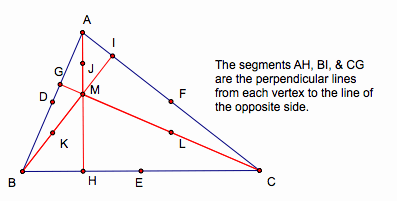
Then, find the midpoint of the segment of each altitude from its vertex to the orthocenter

 

 

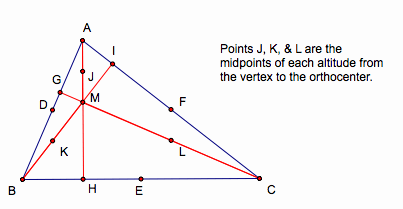
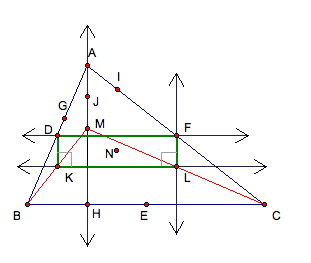
Again, pick any midpoint of each altitude from the vertex to the orthocenter, which are the points J, K, & L, and connect a midpoint of the opposite sides of ÆABC.

 

 

 

 

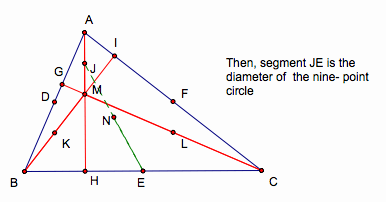
Finally, find the midpoint of segment JE, and that midpoint is the center of the nine-point circle.

 

 

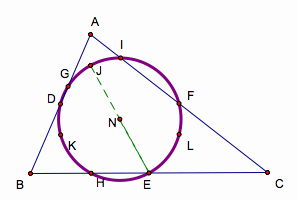
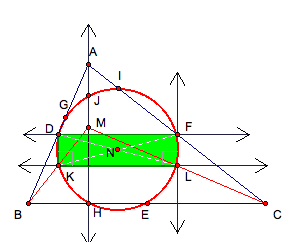
Here is a diagram without orthocenter and altitudes.

 

 

 

 

 

 

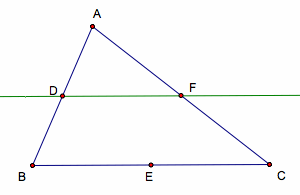
Proof:

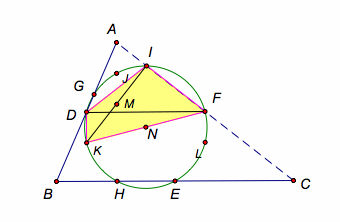
Let D and F be the midpoints of segments AB & AC 

Construct the segment DF by joining the points D & F.

Since the points D & F are the midpoints of sides AB & AC of ÆABC, the segment DF is parallel to the segment BC. (The Midsegment of Triangle Theorem).

 

 

For the same reason,

 

  for the ÆBMA, the segment KL is parallel to the segment BC.

 

 

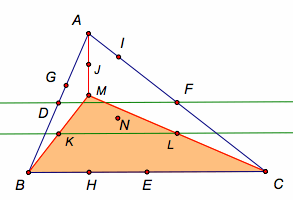
  for the ÆACM, the segment FL is parallel to the segment AM.   

 

 

Similarly, using the ÆCBM, the segment DK is parallel to the segment AM.  Therefore, the segment FL is parallel to segment DK. (Transitive property).

 

 

 

Furthermore, the segments FL and DK are perpendicular to the segment DE & KL since AH is perpendicular to the segment BC.  Thus, DFLK is a rectangle. (Definition of rectangle)

 

 

 

 

 

 

 

 

 

Then, the point N is the center of rectangle DFLK since itÕs the intersection point of the two diagonals DL & FK; it follows that the point N is equidistant from the four corners.

Hence, the points D, F, L, & K lie on a circle N with center N. 

 

 

 

 

 

 

 

NEXT, we want to show that this circle contains the other required points.

 

DKIF is a cyclic quadrilateral because the angels KDF & FIF subtending FK are both right angles.  Since the circle is determined by three points, this circle is the same as the circle N; in other words, the point I lies on the circle N.

 

Note: A cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. In a cyclic quadrilateral, opposite angles are supplementary.

 

 

Similarly, we can prove that DGFL is a cyclic quadrilateral, and so the point G lies on the circle N.

 

 

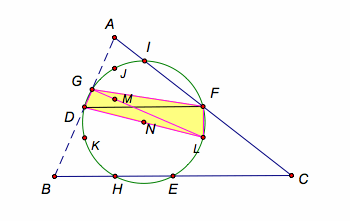
Now, shifting to the segment AC as the base of the triangle, the same argument shows that DJLE is a rectangle, with the same center N, since the point N is the midpoint of the segment DL.  Therefore, the points J and E also lie on the circle N.

 

 

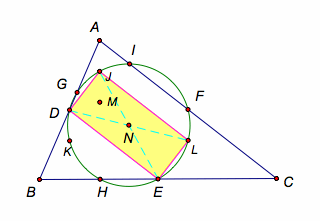
Finally, HDJE is a cyclic quadrilateral for the same reasons as above, so the point H is also on the circle N.  

 

 

 

 

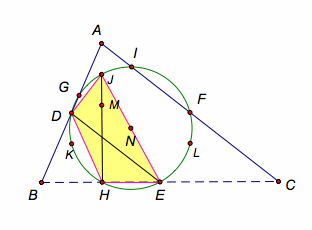
 QED.

 

 

 

Return to Jane's Homepage