
Constructing
a Triangle with Three Medians
by
Jane Yun
Median
Concurrency Theorem
The three median of any triangle are
concurrent; that is, if ÆABC and D, E, & F are the midpoints of the sides
opposite A, B, & C, respectively, then the segments AF, BD, & CE all
intersect in a common point G. Moreover, AG = 2GD, BG = 2 GE, and CG = 2GF.
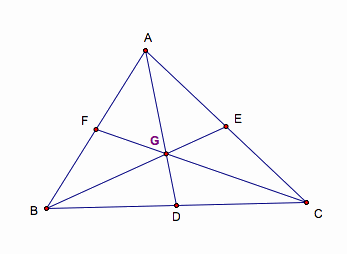
We know that medians trisect each other,
and that trisect point is called centroid. The centroid (G) of a triangle is the common intersection of
the three median points. The
median of a triangle is the segment from a vertex to the midpoint of the opposite
side.
We will explore and investigate how to
construct a triangle with three segments that are medians.
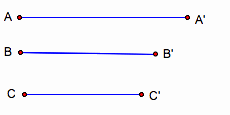
Here are the give three segments that are
medians.
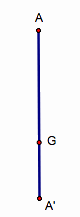
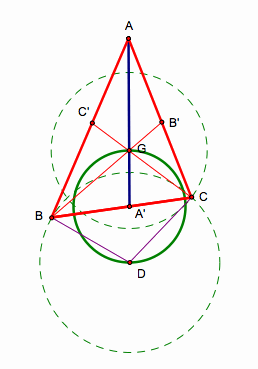
Draw the median AAÕ, and mark the
centroid G, which the 1/3 of the distance from AÕ to A.
Extend AAÕ to D, so that GAÕ = DA'.
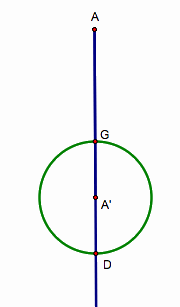
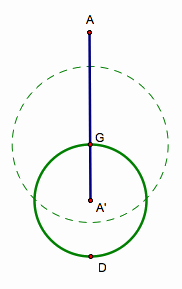
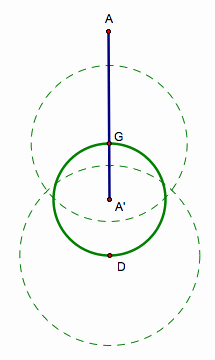
Draw a circle with the center G and radius 2/3 of CCÕ.
Again, draw a circle with center D and
radius 2/3 of BBÕ.
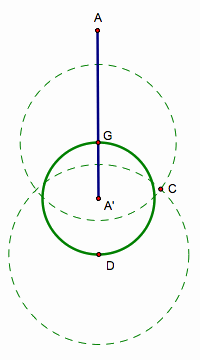
Then, these two circles intersect at point
C,
And we can locate B in any of several ways
and draw the ÆABC.
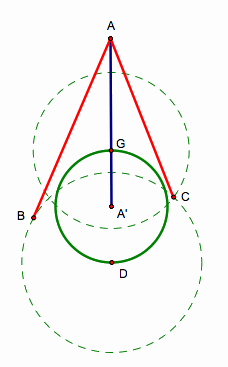
In our finish construction, quadrilateral
BGCD will be a parallelogram, where the segments GD & BC are the diagonals
bisect each other.
Want to see my GSP and check my work!! Click here.
Also here is my proofÉ
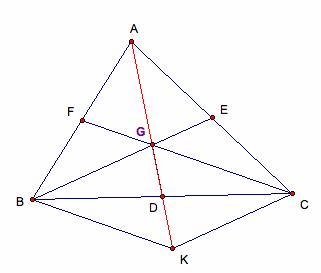
Given:
In ÆABC, the median BE & CF intersects at G. AG is joined and produced to meet BC in
D.
Prove that AD is the median, the segment BD
= the segment DC, and the ratio of AG:GD, BG:GA,GE:CG
is 2:1
Proof:
Produce AD to K such that AG=GK. Join KB and KC.
First, we want to show that the segment AD
is the median, so it divides the segment BD into BD = DC.
Then, in ÆABK, F is the midpoint of AB
since CF is the median, the segment CF makes the point F is the midpoint (by
definition of median).
G is the midpoint of AK by the
construction.
Therefore, FG║BK or GC║BK (by
the theorem on line joining the midpoints of any two sides of a triangle.)
Similarly, in ÆACK, GE║CK or GB║CK
and GE = ½ CK
Since GB║CK & GE = ½ CK,
BGCK is a parallelogram.
Since BGCK is a parallelogram, the segments
BC and GK are diagonals.
And, the diagonals of a parallelogram
bisect each other,
so
the segment BD = DC.
Therefore, the segment AD is the median
from A since the BD = DC and by the definition of median.
Next, I want to show that the ratio is the
2:1.
Since GK and BC are the diagonals of BGCK,
GD = DK.
So it follows that GD = ½ GK and GD
= ½ AG.
Therefore, the AG:GD
= 2:1.
Similarly, we can prove that BG:GE = 2:1 and CG:GF = 2:1.
Therefore, the segment AD is the median of ÆABC
and AG:GD = BG:GE = CG:GF = 2:1.
QED