When the Pedal Point is the Orthocenter

by

Jane Yun

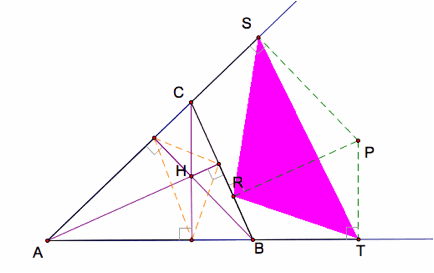
To construct a pedal triangle, let P be any point in the plane. Draw the perpendicular lines from the point P to the sides of ∆ABC. If the point P is the outside the triangle, extend the sides of ∆ABC. Then, let R, S, & T be the points of those intersection.

The triangle ∆RST is the pedal triangle associated with ∆ABC and the point P.

Click here for the GSP script tool for the general construction of pedal triangle to ∆ABC, where P can be dragged any point in the plane.

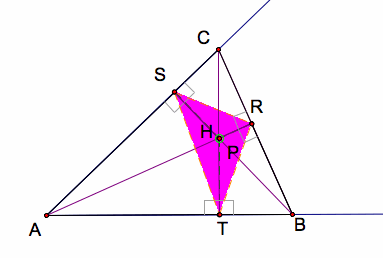
Let investigate when the pedal point P is the orthocenter, where it lies inside the triangle; that is, the triangle is not an obtuse. Recall that the orthocenter of a triangle is a single point where three altitudes meet.

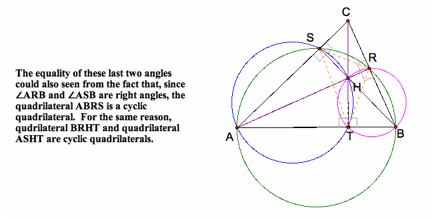
We see that when the pedal point P is located at the orthocenter, the pedal triangle, ∆RST, is called the orthic triangle or altitude triangle - the triangle joining the feet of the altitudes of a triangle. Also, the incenter of the orthic triangle is the orthocenter of ∆ABC.

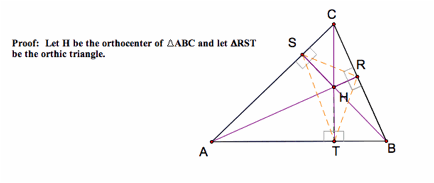
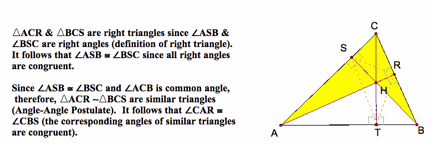
Here is proof that the orthocenter, H, of ∆ABC is the incenter of the orthic triangle, ∆RST.

If DABC is an obtuse triangle, and the pedal point P is the orthocenter, then the pedal triangle is still the orthic triangle, and the incenter of orthic triangle is the orthocenter.

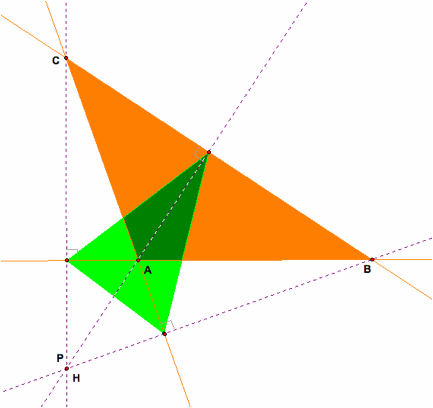
The partial part of pedal triangle lies outside the triangle. This is acceptable result since the orthocenter lies outside the DABC.

---

Return to Jane's Homepage

---