G R A Z I N G   A R E A

by

Jane Yun

 

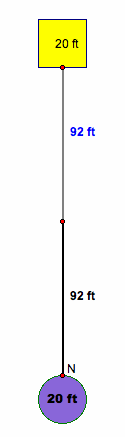
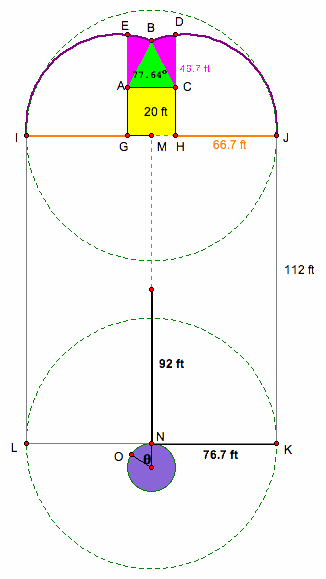
Farmer Jones had a goat on a tether.  He tied the end of the tether not attached to the goat to a stake in the field.  In the field, there are a shed that is 20 feet long and 20 feet wide, which is a square, and a silo that is 20 feet in diameter.  The center of the shed and the center of the silo are on a line and the distance apart is 92 feet.   The total distance between a shed and a silo is 112 feet.  Over what area could the goat graze?

 

 

 

 

 

 

 

 

When the goat moves to M, which is on the center of one of the sides of shed, the figure shows the shape of the grazing area.  The shape of the grazing area is a semicircle with a little area out of it.

 

 

 

 

 

 

     

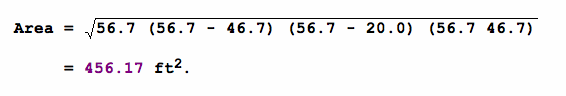
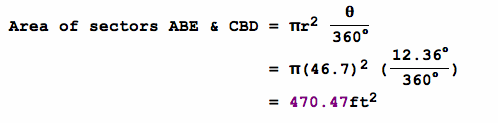
The diameter of the silo is 20 feet, so the radius of silo is 10 feet.  The length of tether is 76.7 ft.

 

d = 20 ft           r = 10 ft           L = 76.7 ft

 

When the goat is at the end of his tether on the silo side of the tangent point N, the tether runs along the silo until some point O.  Then, the going goes off in a straight line, and the remainder of the tether lies on the tangent to the circle at O.

 

Consider the central angle between N and O, and letÕs call this angle θ radian. 

 

           

 

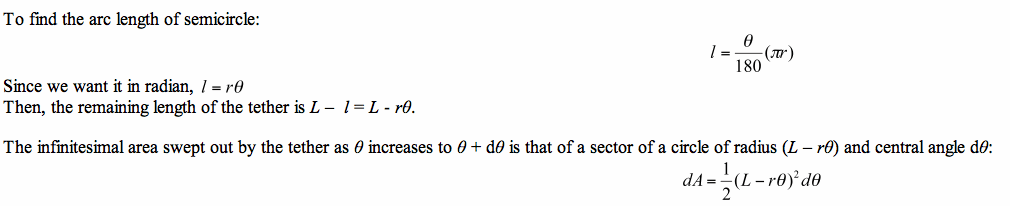
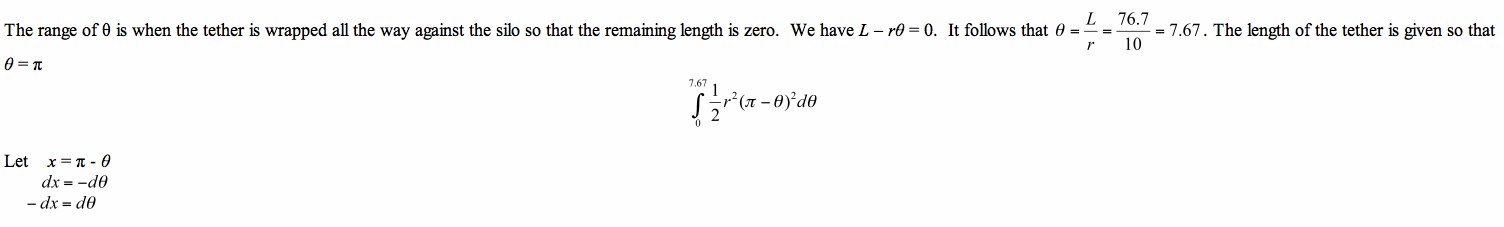
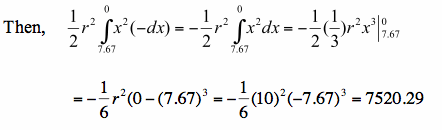
Hence, the area that the goat can graze is approximately 7520.29 ft.

 

The total area that the goat can  graze as follows:

  Area of DHJ & EGI + Area of ÆABC + Area of sectors ABE & CDB + Area of rectangle IJKL + Area of around the silo = 6988.30 + 456.17 + 470.47 + 14112.80 + 7520.79 = 29548.53 ft2.

 

Therefore, the total area that the goat can graze is approximately 29548.53 ft2.

 

 

Return to Jane's Homepage