P a r a b o l a

By

Jane Yun

---

We know how to graph the quadratic equation y = x². Then, we will explore what is changing when we change the values of ‘a ‘.

Figure 1

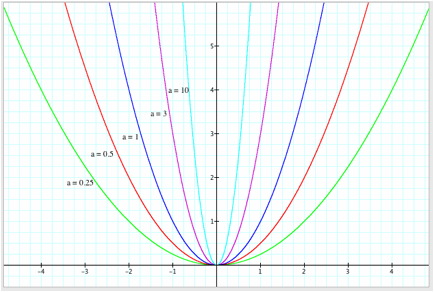
Figure 1 shows the graph of four functions of the form y = ax² when a > 0,

a = ¼, a = ½, a = 1, a = 3, and a =10.

Notice that the larger the value of a, the “narrower” the graph, and the smaller the value of a, the “wider” the graph.

Figure 2

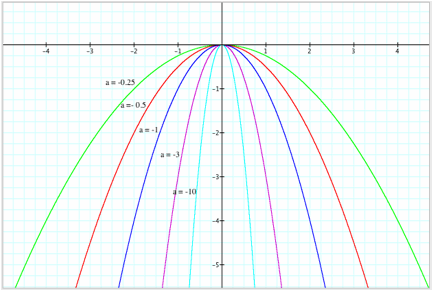
The next Figure 2 shows the graphs of y = ax² when a < 0.

a = - 1/4, a = -1/2, a = -1, a = -3, a = -10.

Notice that these graphs are reflections about the x-axis of the graphs in Figure 1.

Based on the results of these two figures, we can draw some general conclusions about the graph of y = ax². First, as │a│ increases, the graph becomes narrow (a vertical stretch), and as │a│ gets closer to zero, the graph gets wider (a vertical compression). Second, if a is positive, then the graph opens up, and if ‘a’ is negative, the graph opens down.

Figure 3

The graphs in Figures 1 & 2 are typical of the graphs of all quadratic equations, which we call parabolas. Refer to Figure 3, where two parabolas are pictured. The one on the left opens up and has a lowest point; the one on the right opens down and has a highest point. The lowest or highest point of a parabola is called the vertex. The vertical line passing through the vertex in each parabola is called the axis of symmetry of the parabola.

---

Returen to Jane's Homepage

---