
Math 6680 –
Jackie Gammaro
Assignment #1 - Problem
#3
Find two linear
functions f(x) and g(x) such that their
product h(x) = f(x)Šg(x)
is tangent to each of f(x) and g(x) at two distinct points. Discuss and
illustrate the method and the results.
I. Problem Solve - Trial and Error
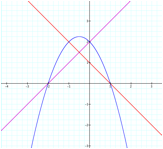
After a few tries, I let f(x) = 2x + 4 and g(x) = -2x - 3, thus their product h(x) =(2x + 4)(-2x - 3).
The following is a graph of f(x), g(x), and h(x).
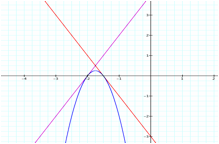
II. What are the equations?
After this little success I tried to generalize. I noticed the slopes of the two linear
functions were opposites of each other and that their was a relationship
between the y-intercepts of f(x) and g(x).
Thus I let f(x) = mx + b, g(x) = -mx – b + 1, and h(x) = (mx + b)( -mx – b + 1). Below is the graph of these functions. Note: Graphing Calculator 3.5 chooses specific values for m and b. In this case m = 1 and b =1.
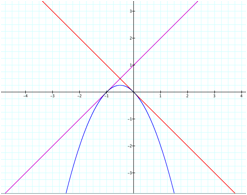
III. “What are the points of intersection?”
I noticed the intersections of f(x) with h(x) and of g(x) with h(x) lie on the y-axis, thus when the functions equal zero. How can I show this
algebraically?
If f(x) = mx + b, g(x) = -mx – b + 1, and h(x) = (mx + b)( -mx – b + 1), to find the points of intersection, determine when f(x) = h(x) and when g(x) = h(x).
f(x) = h(x) g(x)
= h(x)
mx + b = (mx
+b)(-mx –b+1) -mx-b+1 = (mx+b)(-mx-b+1)
1 = -mx –b+1 1 = mx + b
0 = -mx
-b 1-b
= mx
x = ![]() x =
x = ![]()
f![]() =
= ![]()
![]()
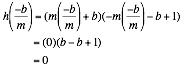
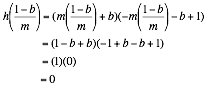
Thus, the points
of intersection are ![]() and
and ![]() .
.
IV. Do the points of intersection always lie on the x-axis?
I also wondered, and “If they
do, then WHY?”
1. First I examined the graphs of f(x –k), g(x –k) and
h(x – k) and then determined algebraically, that horizontal
translations of the functions don’t change the points of intersection off the
x-axis.
2.
I then
examined the graphs of f(x) + k, g(x) + k and h(x) + k. Just from viewing the graphs in Graphing Calculator, I
determined the stipulation that h(x) has to be tangent to f(x) and g(x) at the
points of intersection was not visible. However, points of intersection do lie
on the x-axis. In this case m, b,
k =1.
3. At this point I wondered, “WHY the x-axis?
I studied the graphs, I studied my algebra, and it wasn’t clicking. Then the lightbulb went off!
I had to determine when f(x) = h(x) and g(x) = h(x) and I know h(x) =
f(x)*g(x).
So I let f(x) = a and g(x) = b, and assuming x ŽŚ, substituted into the previous equations which results to
f(x) = h(x) and
g(x) = h(x)
a = ab
b = ab
a = 0 or b = 1 or a,b=0 b = 0 or a = 1 or a,b=0