Assignment #10 – Parametric Curves

Jackie Gammaro

A parametric curve in a plane is a pair of functions x = f(t), y = g(t) where the two continuous functions define ordered pairs (x,y). (Wilson 2010):-).

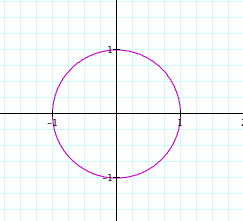
One basic parametric curve defines x = cos(t) and y = sin(t) for value of t from 0 to 2p. One should recognize the unit circle.

To explore the graph in Graphing Calculator 3.5, click on the link below.

Parametric Equation #1

How can we change the equation to explore other graphs?

First, lets investigate x = cos (at) and y = sin (bt) for 0 £ t £ 2p. If a = b = 1, then the graph is the same as above . What if a = b = 2? Somewhat surprising to me at first, we get the same parametric curve. If you’re wondering why, recall sin²x + cos²x = 1, and let x = at, a = b.

I think it will be fun to explore what happens when x = cos (at) and y = sin (bt). Lets vary the values of a and b, such that a ≠ b.

Let a = 1 and let b vary.

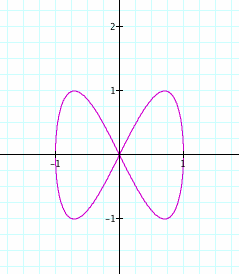
To view in Graphing Calculator 3.5, click on the link.

a = 1, b = 2

Let a = 1, b = 3.

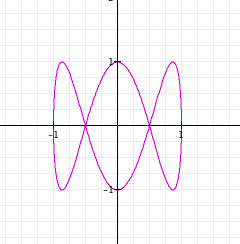
To view in Graphing Calculator 3.5, click on this link.

a = 1, b = 3

Conjecture:

It seems as if, when we fix a = 1, and b = x, where x is an integer, then we have x loops. So the number of “loops” is equal to b. Let b = 5.

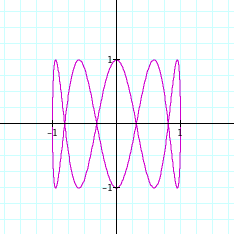
To view in Graphing Calculator 3.5, click on this link.

a = 1, b = 5

It seems as if my conjecture is holding true, one more time.

Let a = 20.

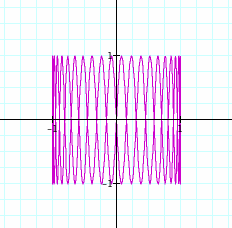
To view in Graphing Calculator 3.5, click on this link.

a = 1, b = 20

II. Let b = 1 and a = x, where x is an integer.

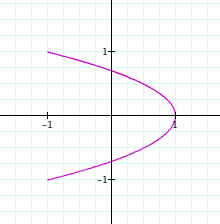
To view in Graphing Calculator 3.5, click on this link.

a = 2, b = 1

Let a = 3, b = 1.

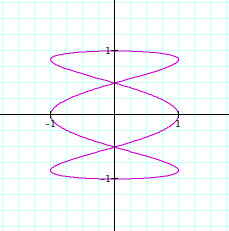
To view in Graphing Calculator 3.5, click on this link.

a = 3, b = 1

This looks like a 90° rotation of the graph when a = 1 and b =3. It seems as if perhaps the number of loops will be dependent upon a, but this time the loops are vertically atop each other, rather than horizontally next to each other.

Lets test the conjecture for a = 4.

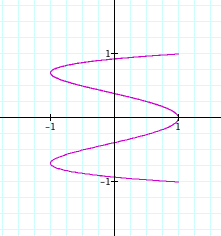
To view in Graphing Calculator 3.5, click on this link.

a = 4, b = 1

Ok, conjecture does not hold true. Now it seems as if when a is odd, it is a 90 degree rotation of the graph when the values of a and b are switched. When a is even, the figure in the graph does not appear to be a closed figure with loops. It seems as if the number of y-intercepts is equal to the value of a.

Lets test this conjecture for a =10, b = 1.

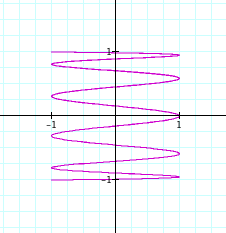
To view in Graphing Calculator 3.5, click on this link.

a = 10, b = 1

Let a = 11.

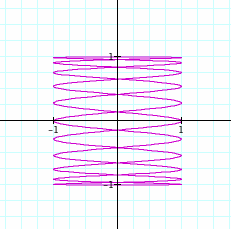
To view in Graphing Calculator 3.5, click on this link.

a = 11, b = 1

It seems as if my conjecture is true.

Now, it’s your turn. Change values of a and b and see what the curve looks like.

So, Ill get you started, just one more! Lets see what happens when a = 4 and b = 5.

Let a = 4 and b = 5.

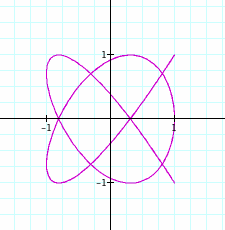
To view in Graphing Calculator 3.5, click on this link.

a = 4, b = 5

Pretty neat is look like a pretzel. Now fix the value of a to be 4, and let b vary, or fix b = 5, and let a vary and make some conjectures, better yet, try to prove your conjecture!

RETURN