
Jackie Gammaro
Centers of a Triangle - Centroid
EMAT 6680 – Assignment 4
The Centroid of a triangle is the point of concurrency of the three medians of a triangle.
A median is the line segment from a vertex to the midpoint of the opposite side.
Exploring with GSP gives ways for students to first explore the centroid. Then, having students create a centroid by pencil and paper construction is an opportunity for students to be able to visualize the centroid as the center of balance for a triangle.
In this lesson I am
going to explore the centroid, and discover how it is the center of balance by
finding areas of triangles created by the medians using GSP. Then I am going to discuss
briefly how to create a pencil and paper construction and use that construction
to balance the triangle at the centroid.
Balancing a Triangle
at the Centroid
LetÕs find out why we can ŌbalanceĶ a triangle at the centroid. If weÕre talking about balance, we can be thinking of the equal areas. So lets examine the areas of the two triangles created by each median.
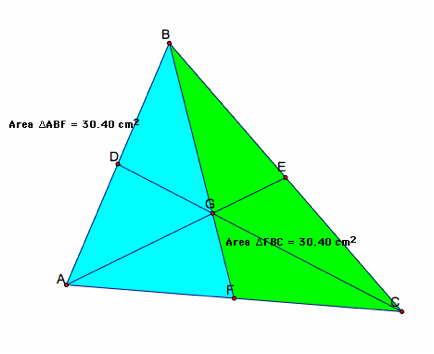
For median BF, lets look at the areas of DABF and DFBC.
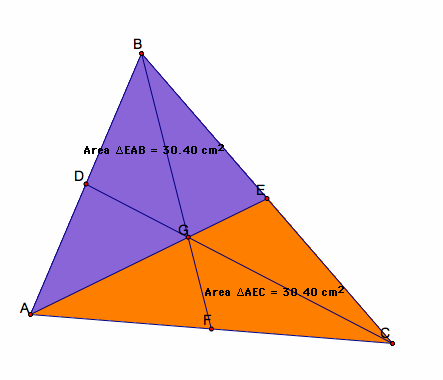
For median AE, lets look at the areas of DAEC and DABE.
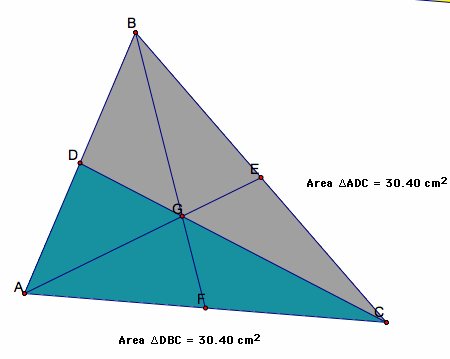
For median DC, lets look at the areas of DDBC and DDAC.
Notice the area of the triangles are all the same value, 30.40sq.units.
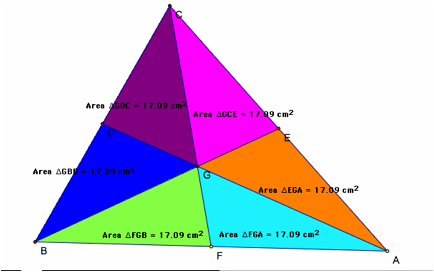
But, IÕm still not convinced. Lets look at the area of the six triangles created by the three medians, whose share the centroid G, as the common vertex of each triangle.
One can notice, no matter the placement of A, B or C, the areas are always equal. Thus, proving to me, that the centroid is the point of equilibrium, or a center of balance.
The
following explanation is how to construct a centroid for a pencil and paper
construction.
1. Draw a
triangle.
2. Place the
compass on a vertex and create a circle whose radius is larger than half the lengths of sides
adjacent to the vertex.
3. Repeat
step 2 with the other two vertices.
4. The
circles will have two points of concurrency, whose line segment will intersect
at the midpoint of each side of the triangle.
5. Mark a
point at each midpoint.
6. Connect
each midpoint with the vertex opposite the midpoint, these line segments are
the median of the triangle.
7. The point
of concurrency for the three medians is the Centroid.
Have
students cut the triangle out and balance the triangle with a sharpened pencil
at the centroid. ItÕs great to see kids fascinated with this concept,
also, it leads to geometric ideas with area of a triangle.