
Jackie Gammaro
EMAT 6680 - Final Project
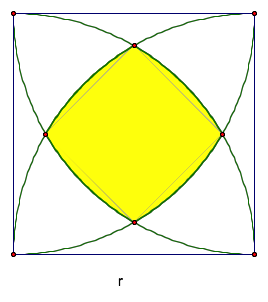
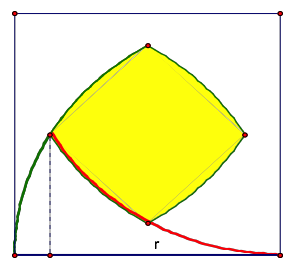
The goal of this write-up is to find the area of the shaded region in terms of the side length r.
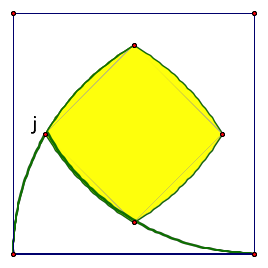
If we can find the area of this outlined section and multiply if by four, we can subtract that value from the area of the square, (r^2) to find the area of the shaded region.
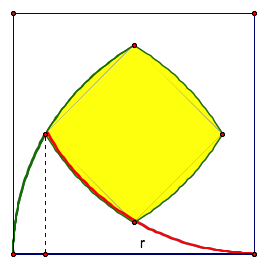
So, if we obtain the area underneath the green curve from(0,0) to j . Then add that to the area underneath the red curve from j to (r,0). That will calculate 1/4 the area of the square that isn't shaded. If we obtain this area and mutiply it by four then subtract that value from s(^2), we will find the area of the shaded region.
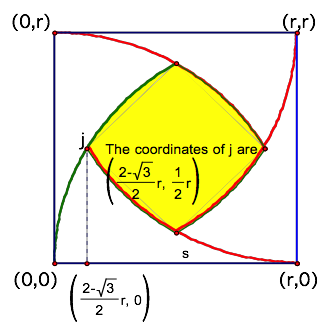
The green curve is part of a circle whose center is (r,0) and has radius, r. The equation of the green curve is (x-r)2 + y2)= r2. The equation of the red curve is (x-r)2 + (y – r)2= r2. The curve sits along a circle with center (r,r) and radius r.
To start solving this, lets parameterize each equation, let![]() .
.
Let ![]()
First, lets find the upper bound and lower bound limits of t.
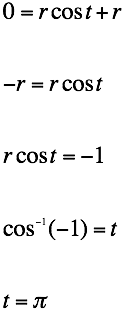
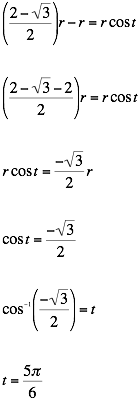
Ok, IÕm going to integrate against my better judgment that from t = p to t = 5p/6
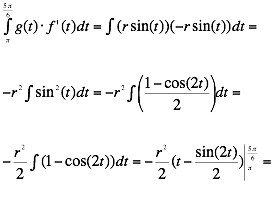
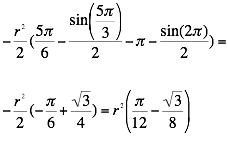
This is the area underneath the curve (x – r)2+y 2 = r2 from x = 0 to
x = ![]() r.
r.
Now we need to find the area underneath the curve (x – r)2+(y-r) 2
= r2 from
x = ![]() r to x = r.
r to x = r.
First, we need to find the limits of integration. We are going to integrate from t = ![]() to t =
to t = ![]() .
.
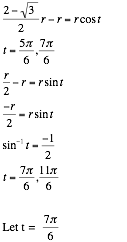
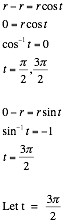
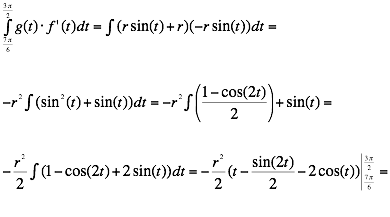
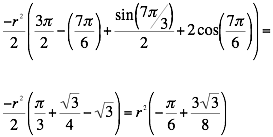
![]()
This is the area underneath the red curve from x = ![]() r to x = r.
r to x = r.
Ok, my brain hurts. Lets rest a moment. Ok, moment over, I want to get this done and get it right, finally!
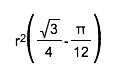
So the area of the sector is ![]()
Now we have to multiply that area by four to get the area of
the part of the square that is not shaded. We obtain ![]() =
= ![]() .
.
So now to obtain the area of the shaded region we will subtract this value from r2, the area of the square.
So, drumroll please, the area of the shaded region is ![]() .
.
![]()