Circles of Apollonius
by:
Brandt Hacker
We generally think of circles as being the locus of points
from a fixed point called the center.
The standard form of a circle is 
. This equation
yields a circle having radius r, centered at the point (h, k). While this is more commonly taught in
geometry, there is another way to define the set of points that create a
circle. The Greek geometer
Apollonius determined that a circle, much like an ellipse has two foci. While on an ellipse, any pointÕs
distance to the two foci of the ellipse is a constant, in a circle it is the
ratio of these foci.
What we will now look to do is examine the relationship between the pedal triangle and the circles of Apollonius. Every triangle has three vertices. If we take one of the vertices and construct a circle that passes through the given vertex but has a constant ratio to the other two vertices, we will have constructed a circle by the definition of Apollonius. In order to do this we start by constructing a triangle.
After constructing this circle we see that every vertex has an internal and external angle in relation to the triangle. To construct the circle we want to bisect both the internal and external angle. We start with vertex B.
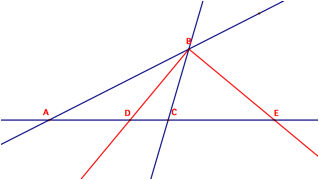
The newly created points, D and E, along with B will create one of the circles of Apollonius. This circle will pass through point B, having foci AC that are in a constant ratio to the locus of points which will create the circle. But how do we find the center of the circle? By creating the circumcenter of triangle BDE we create the circle that passes through all three points. To do this we must first construct the perpendicular bisectors of BD and BE.
The perpendicular bisectors are shown here in black. Their intersection is the circle of our Apollonius circle having foci A and C and passing through point B.
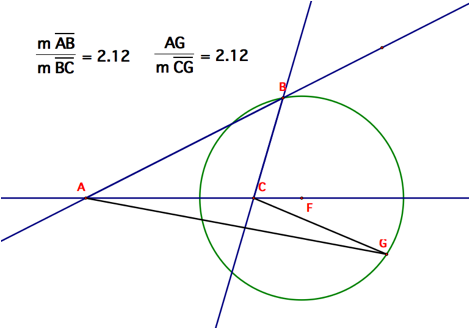
Above is one of the circles of Apollonius for triangle ABC. The black line segments AG and CG are meant to show the ratio that is a constant throughout the locus of points that is circle F.
We create the circles of Apollonius for vertex C and A in the same way. After constructing each of the three circles we are left with the image below.
Circles H and L were constructed in the same way we constructed circle F before. Circle L is a constant ratio from A and B, while circle H is a constant ratio from B and C. What is interesting to note after constructing the three circles is that the three circles share two common points. These points are called isodynamic points.
If we hide the circles we can begin to explore a unique property of the isodynamic points.
In assignment 9 we explored various properties of pedal triangles. For a review of pedal triangles, click HERE. We will now look to explore how the isodynamic points relate to pedal triangles. After constructing a pedal triangle from point P, we see that the pedal triangle, triangle KMJ has many different possible sizes, shapes, and locations.
But what happens if we move the pedal point to one of the two isodynamic points? WeÕll look at Iso1 first.
By moving the pedal point to the isodynamic point, the pedal triangle KMJ becomes an equilateral triangle. The same holds true for the second isodynamic point.
For a GSP file allowing you to change the size of triangle ABC and pedal point p, click HERE.
Return to Hacker