Area Common to Four Circles:

 

by:

 

Brandt Hacker

 

For this assignment we are asked to find the area of the shaded region pictured below:

 

 

For a GSP file containing this image, click HERE.

 

The image above is a square with a quarter circle arc from each corner.  The enclosed region of the four quarter circle arcs is the region shaded in yellow.  In order to fully understand the problem we will expand the image above to include the four circles in their entirety.  The shaded region will also be removed in order to avoid the clutter of multiple shaded regions as we work through the problem.

 

 

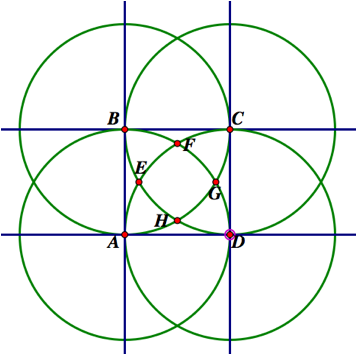
By showing the image construction in its entirety we see more clearly that the corners of the square are the centers of the four circles.  Therefore, if we call any side of square ABCD ÒsÓ, we may also refer to the radius of any circle above as s as well.

 

We start by drawing line segments from D to points E and F.  Along with this a chord EF will need to be drawn as well.

 

 

By constructing the triangle, an enclosed region is created between arc EF and line segment EF.  To find this region is must be noted that EDF is not only a triangle but also a sector.  The measure of  as it is one third of .  We know this because ADC forms a right angle and chords AE, EF, and FC are congruent, forming congruent triangles.  Because DE and DF are two radii of circle D, they have length s.  The area of sector EDF is then found by setting up the following proportion:

 

 

 

 

 

 

 

We see two important regions in this sector.  One is triangle EDF.  The other is the region between arc EF and chord EF.  If we take the area of the sector and subtract the area of triangle EDF, this will yield the area enclosed between circle D and line segment EF. 

 

So, how do we go about finding the area of triangle EDF.  Due to the fact that ED and FD are the same length, we know that EDF is an isosceles triangle.  Since angle D is 30 degrees, the two base angles will each be 75 degrees.

 

This triangle is shown below

 

If we draw a perpendicular from D to FE, we get two congruent right triangles that we may have an easier time working with.

 

 

We are now able to find segment DM and ME by using basic trigonometry.

                       

 

 

 

 

The square root expressions above are equal to their respective values for sin.

Because M is the midpoint of FE, we can now find the length of FE.

 

 

 

 

 

 

From this we can find the area of triangle FDE.

 

Area of triangle FDE:

 

 

 

 

 

 

 

 

Once we know the area of the triangle we are able to find the area of arc segment FE by taking the area of sector FDE and subtracting triangle FDE.

 

Area of arc segment FE:

 

 

 

 

 

 

The area just found, that of the small arc segment, is highlighted in yellow in the image below.

 

 

From the image above we see that there are three other arc segments that could be found in the same way.  They are pictured in the image below.

 

 

We have now found the most difficult region needed to solve the original problem.  The remaining section is square EFGH.  We found the length of line segment FE earlier to be .  By squaring this value, we will have the area of the square EFGH.

 

 

 

 

 

Now that we have the area of the square as well as the area of the 4 arc segments, we can add them all together to find the area of the shaded region the problem was asking for.

 

 

 

 

 

 

 

 

 

Return to Hacker