Assignment 4:

Concurrence of Medians

by
Jenny Johnson

Medians

A median of a triangle is the segment from a vertex to the midpoint of the opposite side. Each triangle will have three medians – one segment from each of the three vertices. One median is shown as a dotted purple segment in the triangle below.

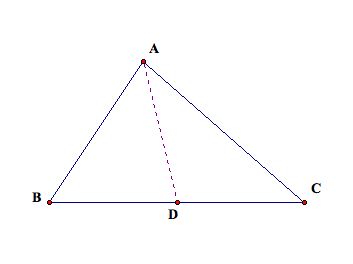
The CENTROID (G) of a triangle is the common intersection of the three medians. In order to construct the centroid, we only need to construct 2 medians and find their intersection. Since the three medians are concurrent, the third median will intersect the other two at their intersection. However, we will construct all three medians for instructional purposes. Their intersection is the centroid (G).

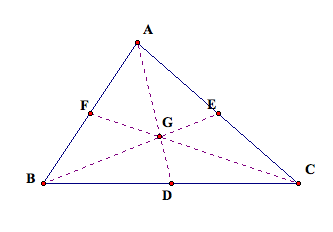
Proof that medians are concurrent

While the picture on Geometer’s Sketchpad demonstrates that the medians are concurrent at a single point, it does not prove that they will always be concurrent. Firstly, it is fairly obvious that the medians of any triangle will intersect inside the triangle. Since the median of any side of the triangle will always be contained on the segment that forms the side of the triangle, then the segment connecting that median to the opposite vertex will also necessarily be on the interior of the triangle. The point of concurrency of the medians of an acute triangle is pictured above. The centroids for an obtuse and a right triangle are pictured below.

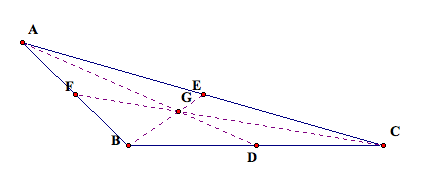
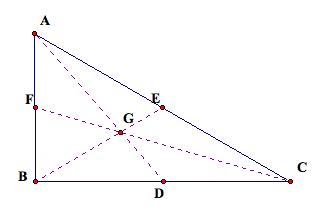
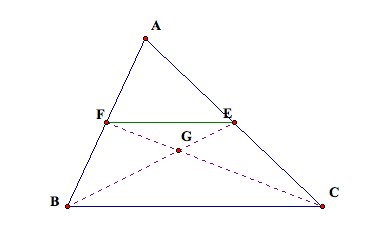
In order to prove the concurrency of the medians, let us start with triangle ABC. Now, let us construct E to be the midpoint of AC and F to be the midpoint of AB. We can also construct the segments BE and CF. We know these two segments will intersect. Let’s call their point of intersection G. Form segment FE.

Segment FE is called the midsegment of the triangle because it is the segment that connects the midpoints of two sides of a triangle. Since it is the midsegment, we know it is parallel to the third side BC and half the length of BC. Since FE is parallel to BC, we know that angle EFG is congruent to angle GCB by the alternate interior angles theorem. Also by the alternate interior angles theorem, we know that angle FEG is congruent to angle GBC. 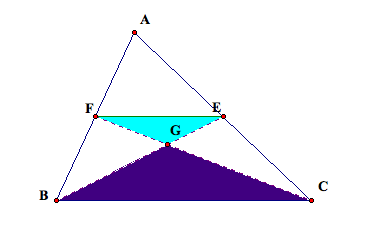Since we know two angles are congruent in triangles FGE and CGB, then the two triangles are similar by the AA Similarity Postulate. The similar triangles are shaded in the picture below.

Since the triangles are similar, their sides are proportional. So,

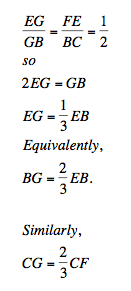
So median CF cuts median BE at a point exactly 2/3 of the way from B to E. Median BE cuts median CF at a point exactly 2/3 of the way from C to F. If we were to construct the midpoint of CB (point D), then the median from A to D must also cut BE at a point 2/3 of the way from B to E. Since we’ve already identified this point as G, then AD must intersect the other two at point G. The diagram below shows the two similar triangles formed when we draw ED as our midsegment.

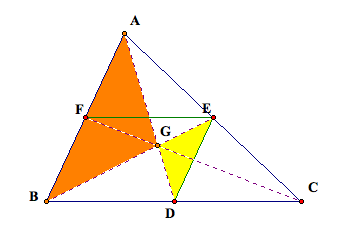
We have thus proven that the three medians in a triangle must be concurrent at a point G and this point is exactly 2/3 the distance from each vertex to the midpoint of the opposite side.

How would GSP help students discover this property of the centroid?

In order for students to make their own discoveries about the centroid, I might give them the following sequence of constructions and questions to explore on GSP:

1. Construct a triangle ABC.

2. Construct the midpoint of BC and label it D.

3. Construct the midpoint of AC and label it E.

4. Construct the midpoint of AB and label it F.

5. Connect A to D, B to E, and C to F. What do you notice about these three segments?

6. Drag A to form different types of triangles. What do you notice about the segments?

7. Mark the point of intersection of the three medians G.

8. Create segments CG and GF. Measure the length of the two segments. Drag A to form different triangles. What do you notice about the lengths of the segments?

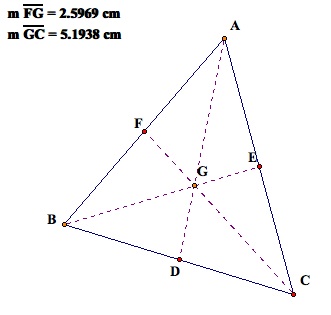
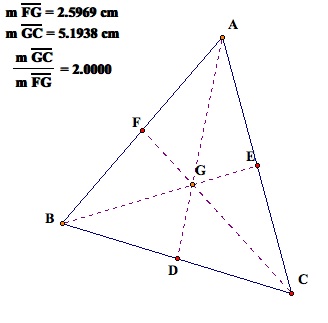
9. Now calculate the ratio of CG to GF (go to the Measure menu, click Calculate, enter CG ¸ GF). Now drag A to form different triangles. What do you notice?

10. Repeat steps 8 and 9 for segments BG and GE. What do you notice?

11. Repeat steps 8 and 9 for segments AG and GD. What do you notice? Do you think this will always be true?

12. How could we be sure that G will always have the same properties you’ve noticed here? Is there another point in the triangle ABC that could have the same properties G has? If so, what point? If not, what does that say about G?

13. Summarize your findings and conjectures about the medians of a triangle and the point where they cross.

Click here for your own exploration of medians and centroids.

Return