Assignment 8:

Orthocenters and Circumcircles

by

Jenny Johnson

What is an orthocenter?

The orthocenter of a triangle is the point of concurrency of the three lines containing the altitudes. An altitude of the triangle is the line segment from a vertex to the opposite side and perpendicular to the opposite side. The orthocenter will not always be inside the triangle. This is why the orthocenter is the point of concurrency of the lines containing the altitudes rather than just the altitudes. Also, the line containing the altitude must be perpendicular to the line containing the opposite side, not just the opposite side as a segment for the cases of obtuse angles.

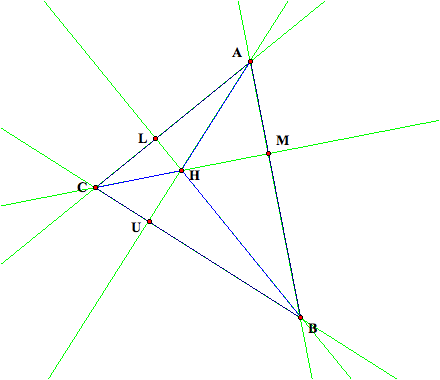
First, I constructed triangle ABC with an orthocenter of H. I made the triangle acute so that the orthocenter would be inside the triangle initially. Since the triangle is acute, the orthocenter lies on the three altitudes. Then, I constructed the orthocenters of triangle HBC (E), triangle HAB (F) and triangle HAC (G). The orthocenter of HBC was just the other vertex of the triangle – A. The orthocenter of HAB was the vertex C and the orthocenter of HAC was the vertex B. I dragged the vertices A, B, and C to form several different types of triangles – isosceles, right, and obtuse – and the orthocenter E was always equal to A, orthocenter F was always equal to C and orthocenter G was always equal to B. Pictures of an acute, right and obtuse ABC are shown below.

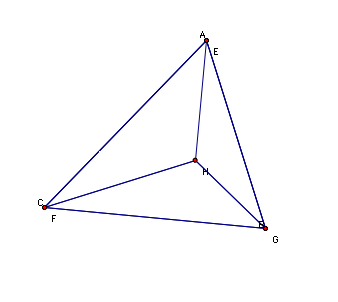
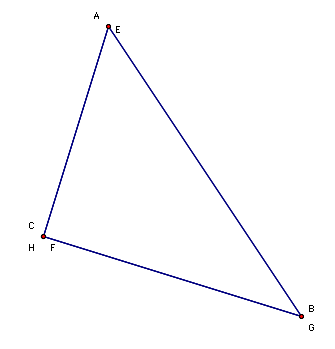
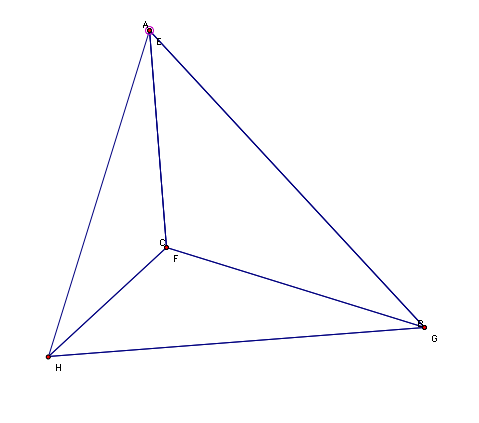
It appears that E = A, F = C and G = B will always be true.

How do we prove it?

I drew the lines containing the altitudes of my original acute triangle ABC. The line containing the altitude from vertex A goes through H and intersects line BC at a right angle. The line containing the altitude from vertex B goes through H and intersects line AC at a right angle. The line containing the altitude from vertex C goes through H and intersects line AB at a right angle.

Now let’s look at triangle AHC. In order to find the orthocenter for this triangle, I would construct the lines containing the altitudes for each of the vertices A, H and C. H, B and L are collinear, so the line BL is perpendicular to line AC, which is the common side to both triangles ABC and ACH. Thus, the altitude HL from H is contained in this line already. Does the altitude need to be unique? Let’s say there is another line that contains an altitude through H perpendicular to AC at a point P. That would form the triangle HLP that has two right angles. This is a contradiction. Thus, there is a unique line that is perpendicular to AC (or any line) through point H (or any given point). This line is HB and contains the altitude from H for triangle AHC. The foot of the altitude from H is L.

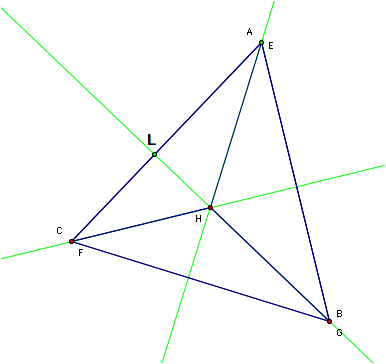
Now, let’s look at the line containing the altitude from A perpendicular to the line containing the opposite side HC. Well, line AB is perpendicular to HC by construction. Since there is a unique perpendicular to a line from a given point, then AB must be the unique perpendicular from A to line CH. The foot of the altitude from vertex A is M.

Finally, the line containing the altitude from vertex C perpendicular to the line containing the opposite side HA must be the line CB since CB is perpendicular to HA by construction. The foot of the altitude from vertex C is U for triangle ACH. Thus, the three lines containing the altitudes of triangle ACH are HB, AB, and CB which all intersect at point B. Point B is therefore the point of concurrency of the lines containing the altitudes (perpendiculars from the vertices of ACH), and hence B is the orthocenter of triangle AHC.

We have proven that the orthocenter of triangle AHC will always lie on the vertex B. Similarly, we can show that the orthocenter of AHB will always be C and the orthocenter of CHB will always be A using the same arguments.

What is a circumcircle?

A circumcircle is a triangle’s circumscribed circle. This means it is the unique circle that passes through the three vertices of the triangle. It is constructed by finding the point of concurrency of the triangle’s three perpendicular bisectors. This point, called the circumcenter, is the center of the circumcircle. The radius is the distance from the circumcenter to any of the vertices.

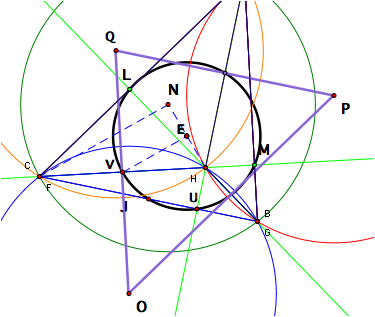
I constructed the circumcircles of triangles ABC, AHC, AHB, and CHB. Then, I connected the circumcenters of the circumcircles for triangles AHC, AHB and CHB to form another triangle. See the picture below.

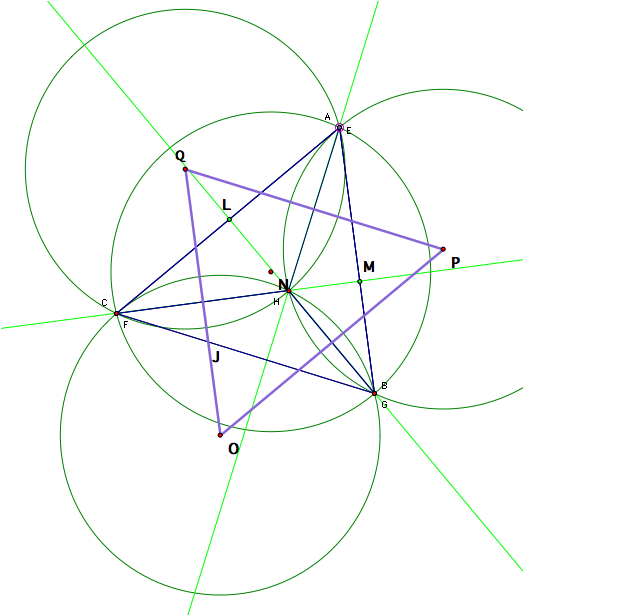
It appears that the circumcenter N of the circumcircle for triangle ABC is also the orthocenter of our newly formed triangle OPQ. I constructed the lines containing the altitudes for triangle OPQ and they intersected at N. Triangle OPQ is congruent to triangle ABC with corresponding sides parallel to each other.

The four circumcircles also appear to be congruent. Now let’s construct the 9-point circle for each of our four triangles. The 9-point circle ends up being identical for all four triangles and is the circle outlined in the picture below.

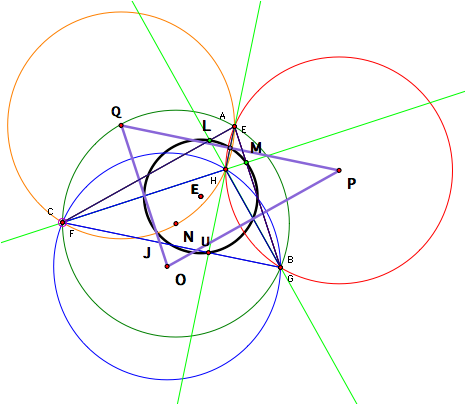
Why is the 9-point circle identical for all four triangles?

Well, for triangle ABC, the 9-point circle goes through the feet of the three altitudes L, M and U. Three points determine a circle. Then the 9-point circle for triangle AHC has to go through the feet of its three altitudes, which are again L, M and U. Similarly, for triangles AHB and CHB, the feet of their altitudes will be L, M and U and therefore they will have the same 9-point circle determined by these three points. Thus, the 9-point circle is the same for all four triangles.

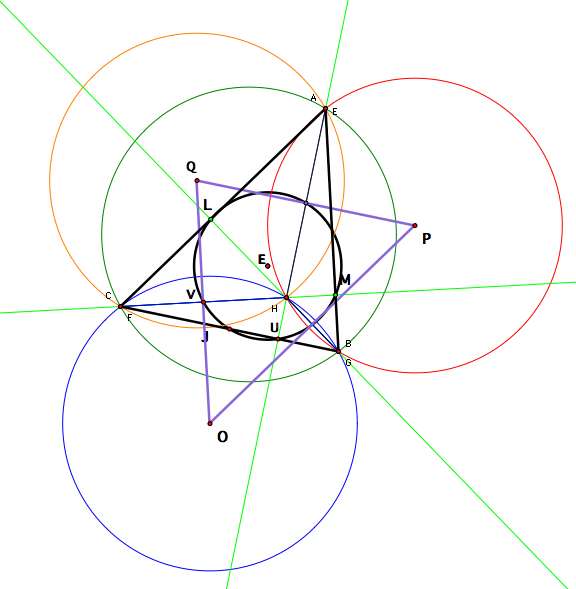
Why are the circumcircles equal?

Now consider the triangle CHN (seen below by a dashed blue line). We know that E is the midpoint of NH since the center of the 9-point circle is the midpoint of the segment connecting the orthocenter with the circumcenter.  Also, point  V is the midpoint of CH since the 9-point circle goes through the midpoint of the segments connecting the orthocenter with the vertices of the triangle.  So, VE is a midsegment for triangle CHN making it parallel to CN and half the length of CN.  Thus, the radius of the 9-point circle is half the radius of the circumcircle.  Since the 9-point circle is the same for all triangles, then the circumcircles must be congruent for all four triangles as well.

Do your own exploration of orthocenter and circumcircles here.

Return