
Final Project Part IIA:
Quarter Circle Arcs
by
Jenny Johnson
1. First, I created
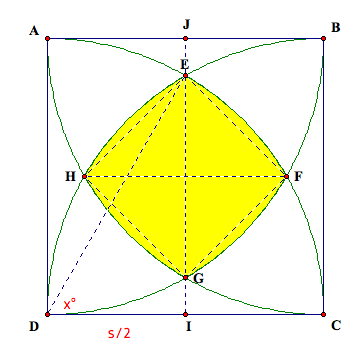
a sketch of GSP of a square with a quarter circle arc from
each corner producing a region bordered by four smaller arcs. A screen shot of the GSP figure is
shown below. To see the file on
GSP, click here.
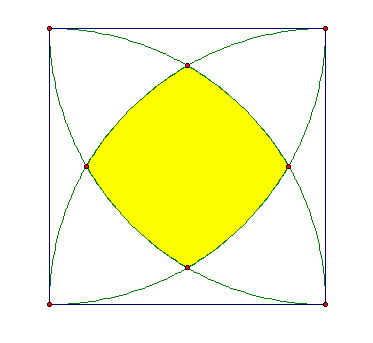
2. Next, I determined the area of the
shaded region of the figure.
It is helpful to see that the figure is
symmetric. If we draw a vertical
line segment exactly halfway between the vertical sides (through the midpoints
of the two horizontal sides), the figure is split into two identical
rectangles, the one a reflection of the other.
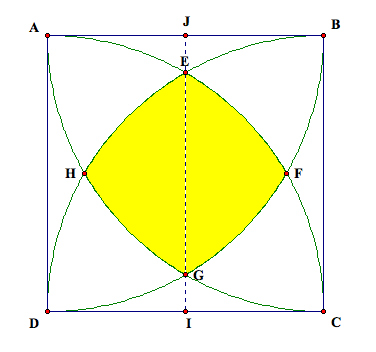
This vertical line goes through E and G. Similarly, a horizontal line through H
and F will cut the square into identical rectangles. Now in order to find the area of the shaded section, we can
find the sum of the area of the quadrilateral EFGH and the area of the
remaining four shaded sectors. Let
us start by finding the area of the quadrilateral EFGH. We can find the length of EG by drawing
right triangle DEI.
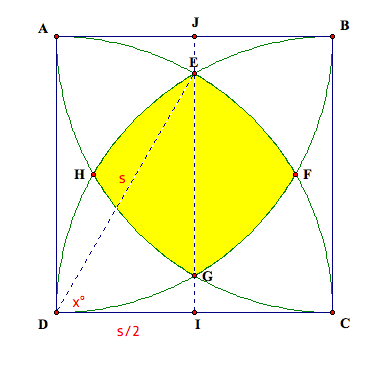
The length of DI will be s/2 since it is exactly
half of the square side s (which is also the radius of the circle centered at
D). DE = s since it is the radius
of the circle. Thus, we can figure
out the angle θ (x in the picture) using
trigonometry.
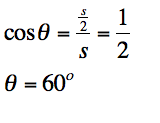
Now that we know the angles and two of the sides of
the triangle DEI, we can find the side EI using trigonometry.
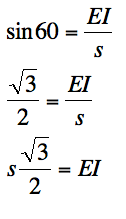
And, since we know JI is length s, we can find
length JE by subtracting JI – EI.
Since the length of JE is the same as the length of GI (by symmetry), we
can then subtract the length of JE (GI) from the length of EI to find the
length of EG. This algebra is
shown below.
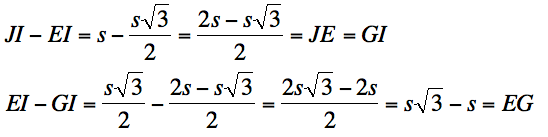
Now that we know the length of EG, let us look at
the quadrilateral EFGH. By symmetry,
we can see the EG = HF (if we did all the calculations for HF that we just did
for EG, we would get the same length).
Thus, the diagonals of the quadrilateral are congruent. This means the quadrilateral must be an
isosceles trapezoid, a rectangle, or a square.
Also, HE = EF = FG = GH by symmetry as well. So, all sides of the quadrilateral EFGH
are congruent. This means it must
be a square because trapezoids donÕt have all four sides congruent. Since this is a square, we know that
angles EFG, FGH, GHE, and HEF are right angles and the diagonals bisect the
angles at the vertices. Thus,
triangle EFG is a triangle with angles measure 45-45-90. This means we can again use some simple
geometry to find the side of the square g. Then the area of the square will just be g2.
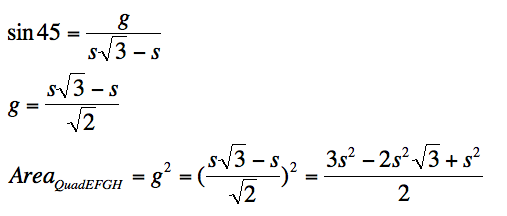
Now that weÕve found the area of the square EFGH, we
can calculate the area of the four shaded sectors that are part of the shaded
region, but outside the square. To
do this, we will create triangle EDF.
If we find the area of the entire sector of the circle (shaded in
orange)
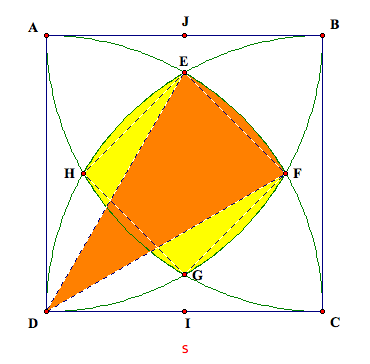
and subtract the area of triangle EDF (orange),
then we will have the area of the section we want.
So, first we want to find the angle measure of
EDF. We know EDC is 600 (shown
above) and that ADF is 600 (by the same argument we made for angle
EDC), so by basic arithmetic, angle EDF = 300. We can then find the area of the whole
sector of the circle (remember r = s).
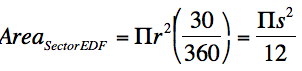
We can also calculate the area of the triangle
fairly quickly using the following formula.
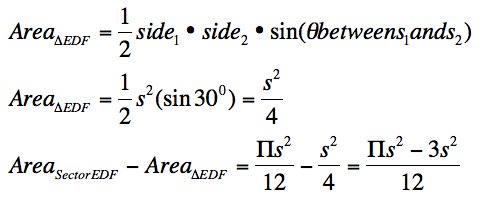
We now have the area of the small sector in the
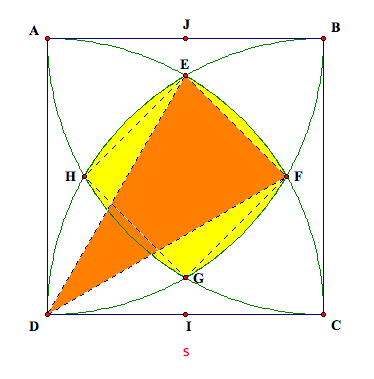
orange-shaded region in the picture below.
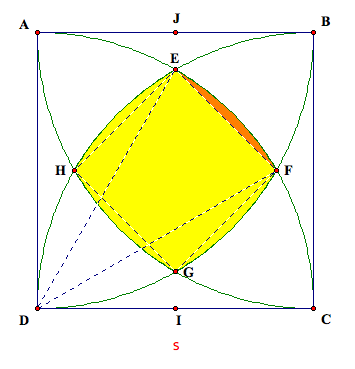
By symmetry, we see that the area of the four shaded
regions we need (shaded in blue below) are congruent. Thus, we can multiply the area we got for the orange-shaded
region above by 4 to get the area of all 4.
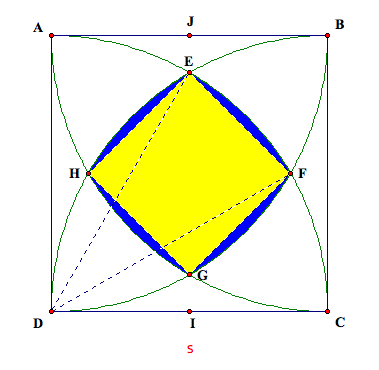
Finally, we can add the area of these four blue
sectors to the area we found for quadrilateral EFGH, and we will have the area
of the entire yellow shaded region.
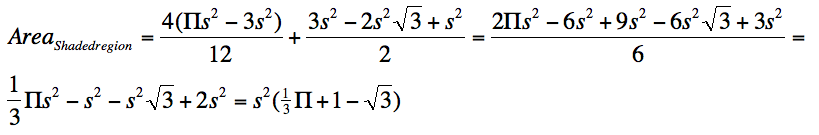
Thus, the total area of the original yellow shaded
region is ![]() .
.