

Around the World: Finding the Golden Ratio
Ashley Jones
So many students ask the question "When will I ever find or use math in the real world?" I encourage these students to research and explore their every day life for examples of mathematics. Whether they are able to recognize it or not, mathematics is usually right under their nose. The Golden Ratio is a great example of mathematics that we encounter almost daily, without even knowing it. This ideal ratio is used by many because of its apparent lure of the human eye. The Golden Ratio has been said to be the most appealing ratio, and is therefore used frequently. Everything from commercial advertising companies, to painters, to even doctors incorporate this 'magical' ratio into their work.
But what is the Golden Ratio? Mathematically speaking, the value of the Golden Ratio is equivalent to ![]() , or about 1.618. This ratio of one plus the square root of five to the value of two can be created using a pencil, compass, and straight edge. We can also use Geometer's Sketchpad to generate the Golden Ratio. Below are the steps to creating your own Golden Ratio using Geometer's Sketchpad. This construction can be used as a demonstration or as an activity for students to explore together as they begin learning about the Golden Ratio.
, or about 1.618. This ratio of one plus the square root of five to the value of two can be created using a pencil, compass, and straight edge. We can also use Geometer's Sketchpad to generate the Golden Ratio. Below are the steps to creating your own Golden Ratio using Geometer's Sketchpad. This construction can be used as a demonstration or as an activity for students to explore together as they begin learning about the Golden Ratio.
Steps to constructing the Golden Ratio:
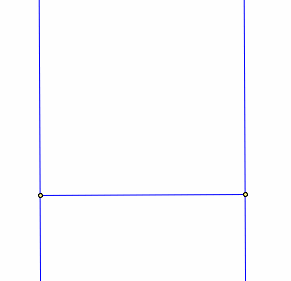
1. Draw a line segment of any length.
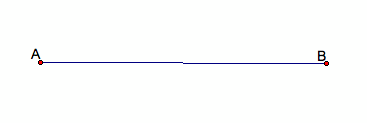
2. Find the midpoint of the segment AB. Create a segment from the midpoint to the point B.
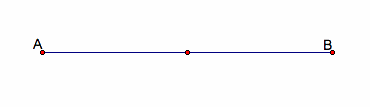
3. Create a line perpendicular to the segment at the point B.
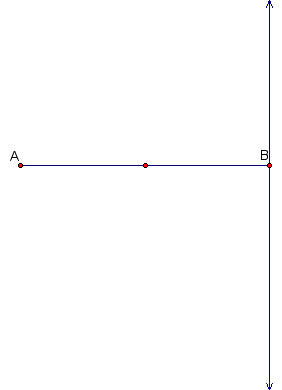
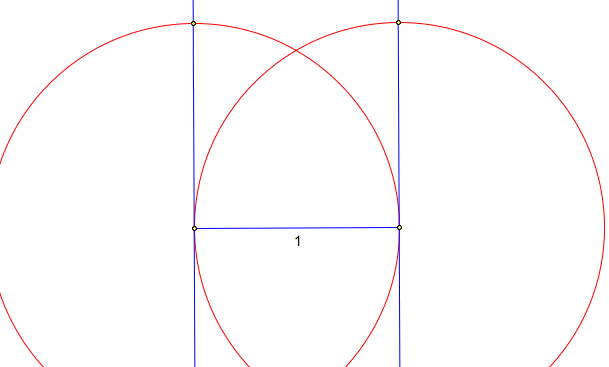
4. Make a circle using the point B as the center, and the midpoint segment as the radius.
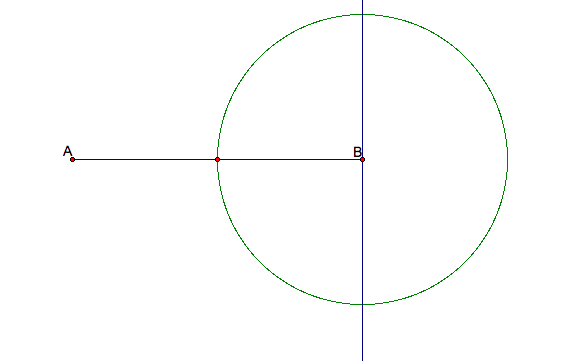
5. Mark the point where the circle intersects the perpendicular line. Draw a ray starting at the point A and going through the intersection point.
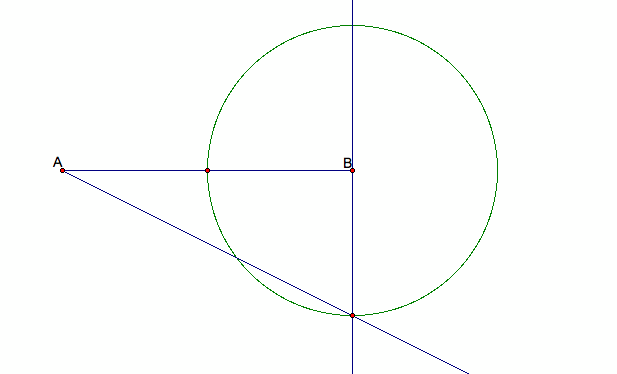
6. Draw one more circle centered at the intersection point with the midpoint segment as the radius. Mark the intersection point of the circle with the ray.
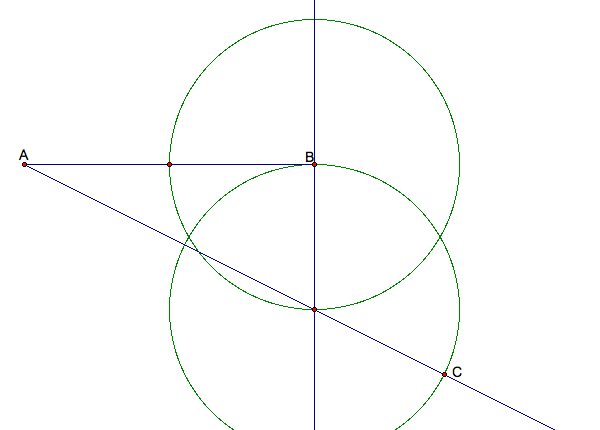
7. The length of segment AC divided by the length of segment AB should give you the value of the Golden Ratio.

I have linked my Geometer's Sketchpad file in which my Golden Ratio tool is included: Golden Ratio Tool
History of the Golden Ratio
Bringing mathematics to life is a great way to really get students interested in the topics. One way to do this is to discuss who, what, where, and when the theorems and/or mathematical topics were discovered. The history behind the mathematics can help students see the topic as more real. Helping students to explore the mathematicians behind the mathematics may encourage them to become more involved with the learning process. The Golden Ratio presents a great opportunity for teachers to ignite interest of its history for students. Have students form groups of three or four, and allow them to research different mathematicians linked to the Golden Ratio. Within the group, students should begin discussing the history of the Golden Ratio with one another. Below is a link for a starter worksheet that could be given to each group to encourage their discussion.
History of the Golden Ratio Worksheet
Students will soon find through their explorations that there is not one date that historians can pinpoint as the discovery date of the Golden Ratio. It is suggested that the ratio was discovered and rediscovered many times throughout history. However, it is also suggested that none of the occurrences of the Golden Ratio were done purposely, but that the structures, paintings, etc. happen to fit the proportion, Phi. The Golden Ratio can be found as being included in structures built by Egyptians, and even in the Bible. Egyptians were said to have used this ratio when constructing the Great Pyramids, while the Greeks used it when designing the Parthenon. The debate of whether the Egyptians and Greeks, among others, actually used the ratio or whether their products happen to fit into the ratio is still frequently discussed. In fact, many people refer to the Golden Ratio as the Greek letter phi, ![]() . Another name that the ratio has been referred to as is the Divine Proportion the 1500's by Da Vinci. It is amazing to research this mathematical topic and see how it interconnects many ideas such as science, art, construction, and many mathematical concepts. Below I have included many interesting occurrences of phi throughout time, and how it shows up in our everyday lives.
. Another name that the ratio has been referred to as is the Divine Proportion the 1500's by Da Vinci. It is amazing to research this mathematical topic and see how it interconnects many ideas such as science, art, construction, and many mathematical concepts. Below I have included many interesting occurrences of phi throughout time, and how it shows up in our everyday lives.
Site used for history information (including pictures): http://goldennumber.net/history.htm

As mentioned before, the Egyptians used phi when constructing the Great Pyramids.

The Golden Section, has been used in art for many years. Seen here, Da Vinci used the Golden Section when creating the portrait of the Last Supper. Key proportions are seen in the above image.

Advertising is another huge avenue where the Golden Number is used. Since so many believe that the proportion is the most ideal to our human eye, it is a great way for advertisers to catch the attention of their customers. The bottles used for soft drinks frequently are created by using the Golden Number. In this image we can see how the label fits into the proportion.

The construction of Notre Dame in Paris also included the use of phi. The blue and white segments illustrate the ideal proportion that was incorporated multiple times.

Greeks referred to the proportion as dividing a line 'in the extreme and mean ratio' which they incorporated when constructing the Parthenon.
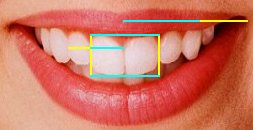
Today, many dentists and oral surgeons use the Golden Section when reconstructing patients teeth. Attractive smiles are said to have the Divine Proportion, sometimes explaining our immediate attraction to another.

Even musical instruments are built with the idea of phi in mind. Illustrated here is the violin and its Divine Proportions.

The Golden Number is frequently found in nature as well. Things such as insects can be found to have the Golden Number when measuring distinct features of the animal.
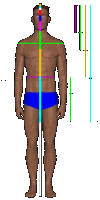
Our own body naturally incorporates phi. Many proportions of various parts of our body allow us to see phi come to life!

We may wonder why some people are so attractive to everyone? The reason is said to be that their face contains many occurrences of the Golden Proportion. George Clooney is believed to have a very 'Golden' face, which could be why so many people are drawn to him.
Using Phi
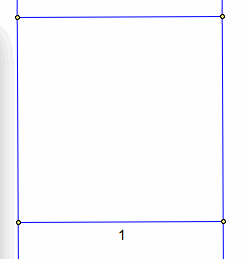
At the beginning of this page, we discussed how to create the Golden Proportion using GSP constructions. Taking this Golden Ratio Tool, we can create 'Golden' geometric shapes. The most basic Golden shape we can create from this tool is the Golden Rectangle. If we do not want to use the tool previously created, we can easily construct a Golden Rectangle from scratch. The Golden Rectangle has side lengths of 1, and base lengths of Phi. This gives us a ratio of sides of Phi/1, which is our goal. Therefore, we will start with a square of side length 1. Begin with a given side length that we will label as length 1.
![]()
Then, to construct your square of side length 1, construct perpendicular lines at the given side's endpoints to the side. Using each endpoint as a center and the side as the radius construct circles to mark of the side length of 1 on the perpendicular lines. Mark the intersection points, and construct a segment from the two intersection points to complete your square of side length 1.

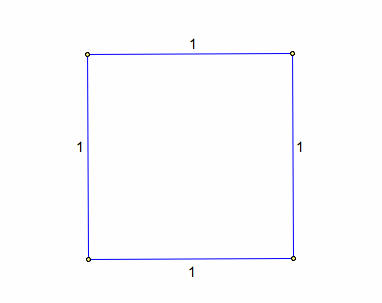
We now have a square of side length 1. We now need to create the side length Phi, by taking similar steps we took to create the Golden Ratio Tool. First, extend a ray from the bottom left vertex and through the bottom right vertex.
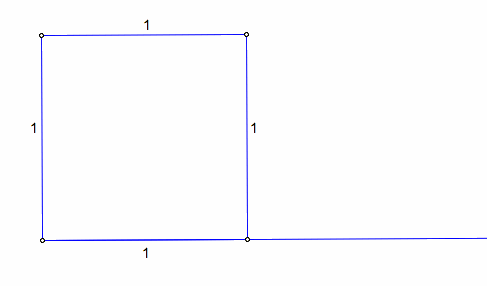
Now find the midpoint of the bottom side, and form the midpoint segment. Create a circle using the bottom right vertex and the midpoint segment. Mark a point of intersection where the circle intersects the parallel line extending from the base of the square.
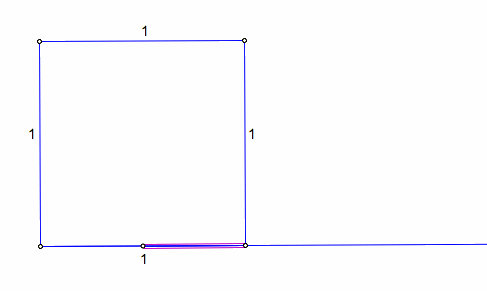
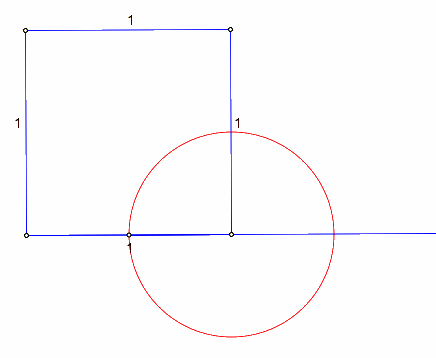
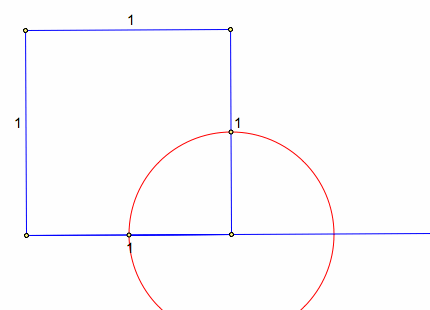
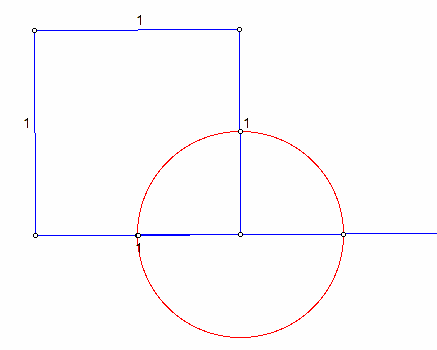
To complete the Golden Rectangle construct a perpendicular line from the point of intersection just made, as well as a parallel line extending the top side of the square. Construct a point of intersection where the two lines cross. This completes your Golden Rectangle.
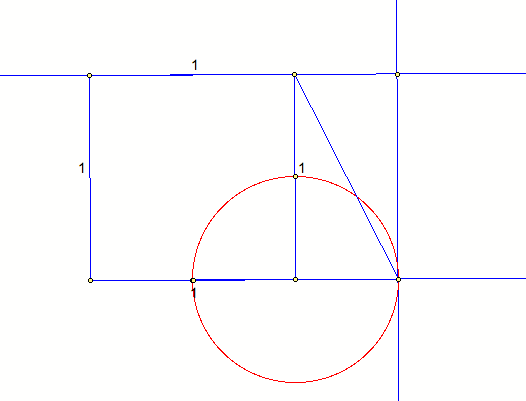
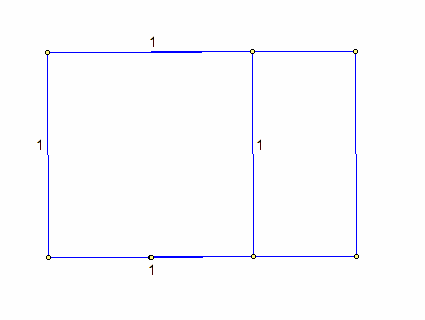
To supplement our Golden Rectangle construction, we can prove that the ratio of the two rectangles is in fact the Golden Ratio. The two rectangles that we are assuming to be similar by the definition of Golden Rectangles, are the red rectangle (with sides equal to (x -1) and 1) and the whole rectangle (with sides equal to x and 1).
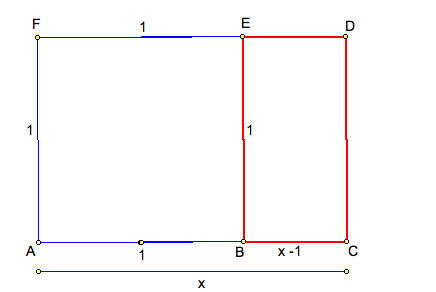
Given that the base of the large rectangle is some value, x, we can begin our proof based on the assumption of similarity.
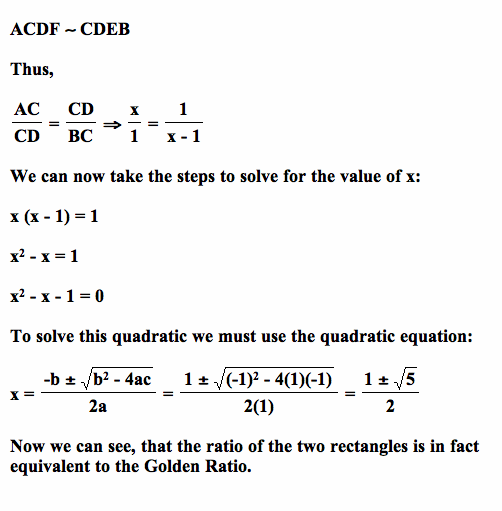
Below I have attached my Geometer's Sketchpad document that includes my tool that allows you to create Golden Rectangles, as well as the proof written out above.
Finding Golden Ratio through Mathematics
Using simple algebra we can compute the value of phi mathematically. When introducing this mathematical idea, you can begin by asking your algebra students to solve the quadratic function, ![]() . This quadratic comes directly from the reasoning described in the section above about the Golden Rectangle. When introducing this function to the students, make sure that you have discussed how it comes from the ratio of sides of a Golden Rectangle (from above). Using the quadratic equation,
. This quadratic comes directly from the reasoning described in the section above about the Golden Rectangle. When introducing this function to the students, make sure that you have discussed how it comes from the ratio of sides of a Golden Rectangle (from above). Using the quadratic equation, 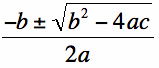 , your students can easily find the value of
, your students can easily find the value of ![]() by themselves. Plugging in the appropriate values from the quadratic function, we can see that
by themselves. Plugging in the appropriate values from the quadratic function, we can see that 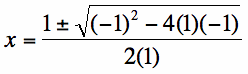 . Thus,
. Thus, 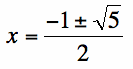 , which is in fact equivalent to the Golden Number of approximately 1.618 for the addition solution.
, which is in fact equivalent to the Golden Number of approximately 1.618 for the addition solution.
Another way to illustrate how you can find the value of Phi mathematically is by using spreadsheets. Programs such as Excel, are a great way to help students understand the mathematics behind a value. With Phi, there are two ways we can use spreadsheets to find the value. The first way is by iterating the function ![]() , when your starting value of 1 is located in the box B2. Then highlight your box containing the function, and fill in the next 20 or so boxes in the column.
, when your starting value of 1 is located in the box B2. Then highlight your box containing the function, and fill in the next 20 or so boxes in the column.
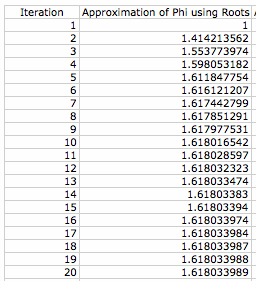
Your students will see that eventually the value you obtain reaches a limit of approximately 1.618, which is in fact the value of Phi. In essence, by having your students use spreadsheets, you are having them illustrate the limit of the series where ![]() . Doing this, not only are you illustrating the idea of Phi, but connecting the mathematical idea of limits. To illustrate the value of Phi using spreadsheet, students can take the same steps, except begin with a starting value of 2 and iterate the function
. Doing this, not only are you illustrating the idea of Phi, but connecting the mathematical idea of limits. To illustrate the value of Phi using spreadsheet, students can take the same steps, except begin with a starting value of 2 and iterate the function 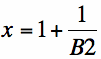 . Again, highlight your box containing the function, and fill in the next 20 or so boxes in the column.
. Again, highlight your box containing the function, and fill in the next 20 or so boxes in the column.
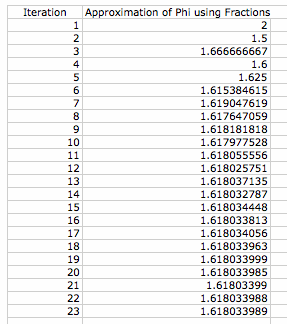
Students will again see that eventually the value you obtain reaches a limit of approximately 1.618, which again is the value of Phi. Now students are finding the limit of the series where 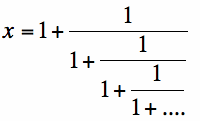 . By doing this in another way, we are connecting the concept of limits even more to Phi. Below I have attached a copy of an Excel spreadsheet file that includes the two approximations of Phi using roots and fractions.
. By doing this in another way, we are connecting the concept of limits even more to Phi. Below I have attached a copy of an Excel spreadsheet file that includes the two approximations of Phi using roots and fractions.
Excel Spreadsheet: Approximation of Phi
Classroom Activity
As teachers we are always looking for new activities and worthwhile tasks to incorporate into our classroom curriculum. When working on the Golden Ratio there are many opportunities to make the material 'come to life.' For this activity students are given the opportunity to create their own Golden Section Gauge. This gauge will allow them to measure various objects, advertisements, and/or things in their everyday life to find examples of the Golden Ratio. I will walk through the steps necessary to construct the gauge. It is a simple construction, and thus easy for students to try without too much difficulty. (This activity has been adapted from the following web site: http://goldennumber.net/goldgrid.htm)
Step 1: Use heavy poster or cardboard to draw four segments of lengths 340 mm, 340 mm, 210 mm, and 130 mm.
Step 2: Cut out each of the four segments. These will be your arms of the gauge.
Step 3: On each of the 340 mm arms, mark off a segment of 130 mm extending from one of the ends of the arm. On the 210 mm arm, mark off a segment of 180 mm extending from one of the ends of the arm.
Step 4: Make small holes at the top of the 340 mm arms (end where the 130 mm segment is marked) and at the segment marks of the end of the130 mm segments, holes at the top of the 210 mm arm (end opposite of the 180 mm segment) as well as at the segment mark of the 180 mm, and holes at each end of the 130 mm arm.
Step 5: Using fasteners that you can get at any office supply store (you will need 4), fasten the gauge in such a manner that the 340 mm arms are on the outside, and the 210 mm arm is to the left of the 130 mm arm.
Above is the complete Golden Ratio Gauge that your students will be able to construct. Encourage your students to find interesting occurrences of the Golden Ratio using their new gauge. I have included a copy of a worksheet that you could use in your classroom to help your students as they work their way through the activity.
We have explored many things relating to the Golden Ratio, however there are many more activities, mathematical exploration, etc. that connect to the Golden Ratio. Find how the Golden Ratio relates to your own personal interests. You'll be surprised to find how the Golden Ratio is connected!